こんにちは。株式会社エル・ティー・エスの渡辺翔太です。今回はこれまでの手法的な話から少し逸れて、確率分布についてお話したいと思います。
確率分布というのは、データがどのように分布しているのかを考える上で重要なものになります。そもそもデータ分析と確率がなぜ関係するのか、確率分布とはそのようなもので、確率分布について知っていると何が嬉しいのか、説明していきたいと思います。
データ分析と確率
データ分析と確率は、一見すると関係ないように感じるかもしれません。また、関係ありそうなのは分かるけど、どのように関係しているのかが分かりづらいといった人もいるでしょう。
なぜデータ分析と確率は関係しているのか。それはズバリ、「世の中のほとんどすべての事象はある確率で起きるものと捉えよう」という思想に基づいているからです。
そして、分析対象となる「データ」は、その事象を記述したものにすぎません。例えば11/30のアイスクリームの売上が10万円だった場合は、「11/30のアイスクリームの売上は10万円」という事象がなんらかの確率で観測されたことを意味します。
そしてデータは事象を記述しているので、
- 11/30のアイスクリームの売上=100000
というようになります。事象の記述の方法はさまざまで、
- 日付=11/30、アイスクリームの売上=100000
- 日付=11/30、商品=アイスクリーム、売上=100000
となったりします。
「ほとんどすべての事象はある確率で起こる」と決めると、次のことが分かります。
- かならず起こる事象は、確率1で起こる事象
- 絶対に起こらない事象は、確率0で起こる事象
つまり、起きるかどうか分からない事象だけでなく、かならず起こる事象や絶対に起きない事象も含めて確率で議論することができます。
データ分析はデータの分布を知るため
ところで、我々はなぜデータ分析をするのでしょうか。それは、究極的にはデータの分布を知りたいからです。データの分布が分かると、
- なぜそのデータが発生したのか(=なぜその事象が起きたのか)
- 今後どのような事象がどの程度の確率で発生するだろうか
という2点について知ることができます。
前者は起きた事象に対して原因を究明することで施策を考えるヒントになります。後者は将来の事象に対して先手を打つヒントになり、機会損失を防いだりリスクマネジメントしたりすることができます。
そして、データは確率的に起こる事象を記述したものですから、データの分布を知ることはつまり、事象の確率分布を知ることと同義なのです。
確率分布とは
データの種類・パターン
それでは、確率分布とは何なのでしょうか。
確率分布を考える際に、データの種類を考える必要があります。
データの種類は次のパターンに分かれます。
- 1つ、2つ…と数えられるものを数えた結果の値
- あるカテゴリをあらわすもの
- 計測した結果の値
①は、ある1時間の来店人数や、5回の試合で何回勝ったかといったデータが該当します。ビジネスのデータでは②を集計したものとして登場することが多いです。
②は来店時の購買の有無、どの商品を購入したか、5段階満足度、などが該当します。ビジネスデータではデータベースに登録されているカテゴリデータなど、非常によく見かけるデータになります。
③は売上などの財務データや気温、湿度などのセンサーデータなどが該当します。数値データはほぼ③に該当します。データベースに登録されている数値データの多くはこれに該当します。
確率分布について
データのパターンを分類したところで、確率分布について考えます。ここで、対象となる事象の名前をX(大文字)とし、事象が取りうる値をx(小文字)とします。
まず、①や②について考えてみましょう。
Xをある1時間の来店人数とします。xは取りうる値ですから、0人の場合もあれば10人の場合もあるでしょう。1時間に1人も来ない確率はP(X=0)と表します。1時間に10人来る確率はP(X=10)です。
1時間にx人来ると考えると、その確率はP(X=x)ですね。このxには0、1、…と無限の整数が入ります。
今度はXを、ある顧客の商品購買行動とします。xの取りうる値は”買う”か”買わない”です。xには数値以外が含まれることもあります。ここでも同じようにP(X=x)を考えることができます。P(X=”買う”)=1/3、P(X=”買わない”)=2/3という具合です。
①や②の場合は、このP(X=x)こそが確率分布と呼ばれるものです。
過去の経験から1時間の来店人数がxとなる確率が1/2x+1と分かっていた場合、P(X=0)=1/2、P(X=1)=1/4、P(X=2)=1/8、…となります。また、これらをひっくるめてxで表すとP(X=x)= 1/2x+1となります。
つまり、確率分布はとりうる値に対応した確率を与えてくれる関数といえます。そして、すべての取りうる値に対して確率の和を取るとその値は必ず1となります。取りうる値のうち、いずれかの値になる確率は1だからです。1より大きくても小さくても確率分布とは言えません。
このように①や②の場合は、ある事象の取りうる値に対して決まる確率そのものが確率分布となります。
一方③の場合は同じように考えてもうまくいきません。
たとえば気温の場合、普段目にする値はせいぜい25.6℃のように小数点第1位までで表されていますが、とても厳密に測定できたとすると25.61552761℃というように表示できるでしょう。
理論的には、真の気温は小数点以下何桁にもおよぶ数値となります。これは、気温が滑らかに変動する実数だからです。
このような場合に、気温をXとしその取りうる値をxとしてP(X=x)を考えることはできるでしょうか。
たとえばx=25.61552761とします。気温がぴったり25.61552761℃になるのはとても珍しいと思いませんか。少しでも値が違ってはいけません。
さらに真の値はもっと小数点以下何桁にもなるのです。小数点以下1000兆桁まで計れる超高性能な温度計で気温を計ったときに、25.000…000℃とぴったり25℃になる確率はほぼゼロです。無限桁まで計れるとなるとその確率はゼロに等しいと言えるでしょう。
このように、ぴったりその値になる確率がゼロであるような場合は、すべてのxでP(X=x)=0となるため、P(X=x)を確率分布とすることはできません。さてどうしましょう。
気温の場合、良く目にする値は少数第1位までの値でした。これは、真の値が25.61552761℃のような場合に小数点第2位を切り捨てているのです。つまり、25.600℃~25.699…℃はすべて25.6℃とみなしているわけですね。
式で表すとP(X[表示]=25.6)=P(25.600≦X[真]<25.7)となります。ここでX[表示]は少数第1位までを表示した気温であり、X[真]は気温の真の値を意味します。
気温が25.6℃と表示されることはよく起こりうることなので確率はゼロではなさそうです。実際に過去のデータから25.6℃となった場合から確率を推定することができます。
③のデータのように取りうる値の範囲を決めると確率が求まるような場合は、確率密度関数という関数によって確率を求めることができます。確率密度関数と取りうる値の範囲によって確率を与える計算式が確率分布になります。
①や②の確率分布は、データが非連続的な値を取るため離散確率分布と呼ばれます。一方③の確率分布は、データが連続的な値を取るため、連続確率分布と呼ばれます。
少しここで奇妙な考え方をしてみます。離散確率分布の場合、P(X=x)を確率分布と呼びました。
たとえばXの取りうる値にaという値があり、その次に大きな値がbだったとしましょう。するとXがaとbの間の値を取ることはありません。つまりP(a<X<b)はゼロになります。そしてP(X=a)がpという確率であれば、P(a≦X<b)=pとなりますね。
離散確率分布でも、事象が取りうる値の範囲とある関数を用いて確率を求めることができます。この関数のことを離散確率分布でも確率密度関数と呼ぶことにしましょう。
以上のことをまとめると、次のようになります。
- 非連続な値をとるデータは離散確率分布に従う。連続な値をとるデータは連続確率分布に従う。
- 離散確率分布は、取りうる値xに対して決まる確率の計算式P(X=x)そのものを指し、これは確率密度関数と同じとみなすことができる。
- 連続確率分布は、取りうる値xの範囲と確率密度関数によって確率が決まる。確率分布と確率密度関数は別物。
- どちらにせよ、事象Xの取りうる値xの値または値の範囲と確率密度関数から確率は計算できる。
なお、Xには一般的な名称があり、確率変数と呼ばれます。
確率分布の種類
抽象的な話が続いたので、具体的に世の中にはどのような確率分布があるのか代表的なものを見ていきましょう。
離散確率分布
離散一様分布
[定義]確率変数Xの取りうる値xについて、すべてのxに対して同じ確率で発生する場合、Xは離散一様分布に従う。
[性質]同じ確率で発生する事象の発生確率を表す。
[確率密度関数]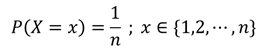
※∈は取りうる値を示す。
[使い方]等確率で選ばれるデータの分布を表す。
ベルヌーイ分布
[定義]確率変数Xの値xが、確率pで1を、確率1-pで0を取る場合、Xはベルヌーイ分布に従う。
[性質]成功確率pの試行を1回行う際に成功または失敗の確率を表す。
[確率密度関数]x=0を代入するとP(X=0)=1-p、x=1を代入するとP(X=1)=pが確認できる。
[使い方]2つに1つの値を取るようなデータの分布を表す。
二項分布
[定義]同じベルヌーイ分布に従う確率変数の和をXとしたとき、Xは確率変数であり、二項分布に従う。
[性質]成功確率pの試行をn回行うとき、成功する回数がx回であるときの確率をあらわす。
[確率密度関数]nCxはn個の中からx個選ぶときの選び方の総数。二項係数と呼ばれる。
[使い方]購入確率が40%の商品を20人の人に見てもらう場合、5人以下の人しか買わない確率や12人以上買う確率を計算できる。また、30人中16人が買った商品の購入確率を推定できる。(直感の購入確率は16/30ですが、それが最も良い推定値であることを示すことができます。)
ポアソン分布
[定義]ある一定の期間に平均λ回発生するイベントが、その期間に発生する回数をXとしたとき、確率変数Xはポアソン分布に従う。
[性質]一定期間に0回、1回、2回、…と数えられる事象に対して、平均λ回発生する場合に、その期間にk回発生する確率を表す。
[確率密度関数]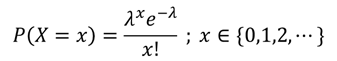
eは自然対数の底(ネイピア数)である。
[使い方]1時間に平均3通メールが来ることが分かっているときに、1時間に1通もメールが来ない確率を求めたり、5分間に平均3人来店することが分かっているときに15分に10人以上来店する確率を求めたりすることができる。
連続確率分布
一様分布
[定義]確率変数Xの取りうる値xについて、同じ長さの任意の範囲にあるxであれば同じ確率で発生する場合、Xは一様分布に従う。
[性質]同じ確率で発生する事象の発生確率を表す。
[確率密度関数]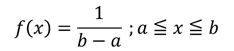 [確率]
[確率]
どの値も等しく発生するデータの分布を表す。特にa=0、b=1のときの一様分布を標準一様分布という。
正規分布
[定義]次の確率密度関数を持つ確率変数Xが従う分布
[性質]平均値付近の値を良く取り、平均値を中心に左右対称となる値は同程度の確率で発生するような分布を表す。統計学では最も基本的な確率分布である。
[確率密度関数]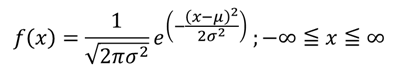
μは平均、σ2は分散(σは標準偏差)を表す。特にμ=0、σ2=1の正規分布を標準正規分布という。
[確率]上記確率密度関数に対して
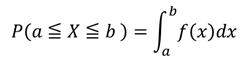
世の中のさまざまな事象は正規分布に従うとされている。また、どのような確率分布を持つ確率変数でも、その平均は正規分布に従うことが知られている。
二項分布で試行回数が十分多い場合や、ポアソン分布で平均が十分大きい場合は正規分布に近づく。線形回帰分析を行なうときには、目的変数は正規分布に従うことが仮定される。
機械学習のパラメータ初期値にも正規分布に従う乱数が用いられる。
指数分布
[定義]ポアソン分布に従う確率変数、つまり一定期間に発生するイベントの回数に対し、あるイベント発生から次のイベントが発生するまでの時間Xが従う分布
[性質]時間の間隔が問題となる事象に対して、ある時間間隔が生じる確率を表す。ポアソン分布の平均がλの場合、指数分布に従う確率変数の平均μについてλ=1/μが成り立つ。
[確率密度関数]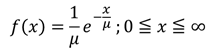 [確率]
[確率]
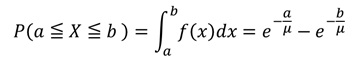 [使い方]
[使い方]
機械の寿命を予測したり、webサイトに1時間後まで次の訪問者が来ない確率を計算したりする。
カイ二乗分布
[定義]標準正規分布に従う確率変数の二乗和Xは、カイ二乗率分布に従う。
[性質]データを変形すると、さまざまなデータがカイ二乗分布に従うことが分かっている。データをカイ二乗分布に従うように変形した上で、仮説検定を行なうことが多い。自由度というパラメータを持つ。
[確率密度関数]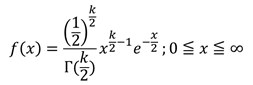 [確率]
[確率]
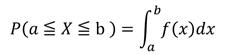 [使い方]
[使い方]
集計表からカイ二乗検定を行う際に用いたり、分散の区間推定をする際の確率分布として使用する。
次回
以上、代表的なものを一覧化してみました。次回は各確率分布をRで扱います。乱数を発生させたり、確率変数の値の範囲から確率を計算したり、確率分布を可視化したりしてみたいと思います。お楽しみに!
アサインナビでは、データサイエンスに関するセミナーを随時開催しております。
過去には、データサイエンティストの知識を習得するための実践塾や、特別講師を招いてのセミナーなどを開催しております。
過去の様子はこちらからご確認いただけます。
▼データサイエンティスト実践塾▼
第1回データサイエンティスト実践塾を修了しました!
▼データサイエンスの現状と未来▼
シリコンバレーに学ぶ、日本のデータサイエンスの現状と未来 ~これからのデータドリブンな時代に本当に必要なこと~を開催しました







