データサイエンティストのお仕事とは？【第10回】主成分分析編

こんにちは。株式会社エル・ティー・エスの渡辺翔太です。今回は主成分分析と呼ばれる手法について学習していきたいと思います。主成分分析は、多次元データの情報量をなるべく保ったまま、低次元化してデータを表現する手法です。

■目次■

主成分分析の概要
irisデータで実践
都道府県別支出データで実践

主成分分析の概要

例えば、10次元のデータ(つまり10列のデータ)を人間は可視化することはできず、傾向を把握することは難しいです。しかし、なるべくデータの持つ情報量を保ったままで2次元や3次元のデータに変換することができると、平面や空間上にデータをプロットし可視化することができます。そのとき、プロットしたデータが数か所にまとまって存在しているといった場合は、元のデータも同じように数か所のクラスターが生じていそうだということが分かります。

主成分分析は、もとのデータから主成分と呼ばれる新たな変数を作成します。この時、主成分は元のデータの線形和(ある数値を掛けて足したもの)として表されます。例えばn次元のデータXがあったとします。

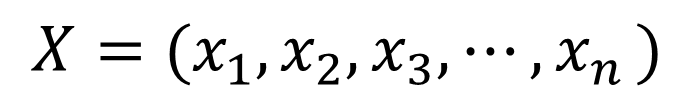
この時、データXが持つ情報量が最も大きい成分をz1、その次に情報量が大きい成分をz2、…というように主成分を計算していきます。

…

…

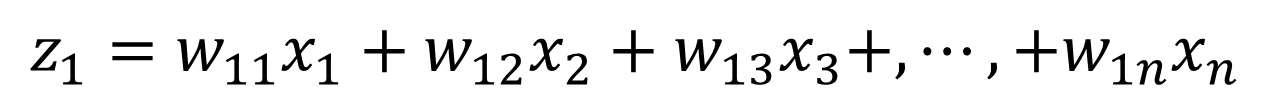
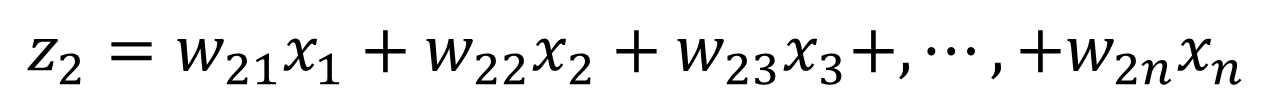
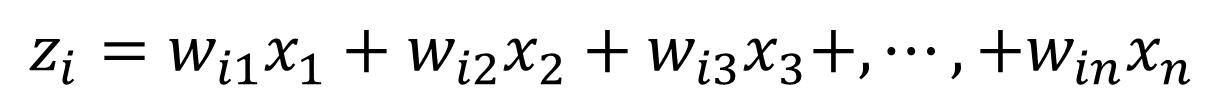
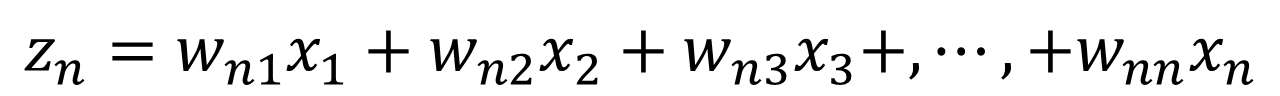
もともとn次元のデータなので、主成分もn次元まで計算することができます。
しかし、目的は情報量をなるべく保ったまま次元を減らすことなので、主成分すべてを用いることはデータそのものをすべて用いることと同じであり意味がありません。
また、Rで主成分を計算することによって、各主成分が全情報量のうちどれだけの情報を持っているかを、割合で算出してくれます。
簡単にirisのデータで実践しながら概要を把握してみましょう。

irisデータで実践

irisのデータは5つの観測データがあり、そのうち4つは実測値データで、残りは花の種類を表すデータです。種類を表すデータは一旦除外し、4次元データとして取り扱いましょう。我々人間は、4次元データをそのまま可視化する方法を持っていません。せめて3次元空間、または慣れ親しんでいる2次元平面にデータをプロットすることで可視化することができます。
平面にデータをプロットする方法のひとつに、2次元のデータを選んでプロットする方法が考えられます。しかしその場合は使用しない残りの2次元データが持つ情報量を失ってしまいます。
そこで、主成分分析を用いて、4次元データから情報量をなるべく保った2つの主成分に次元を削減し、それを平面データにプロットしてみましょう。
まずはデータの準備です。

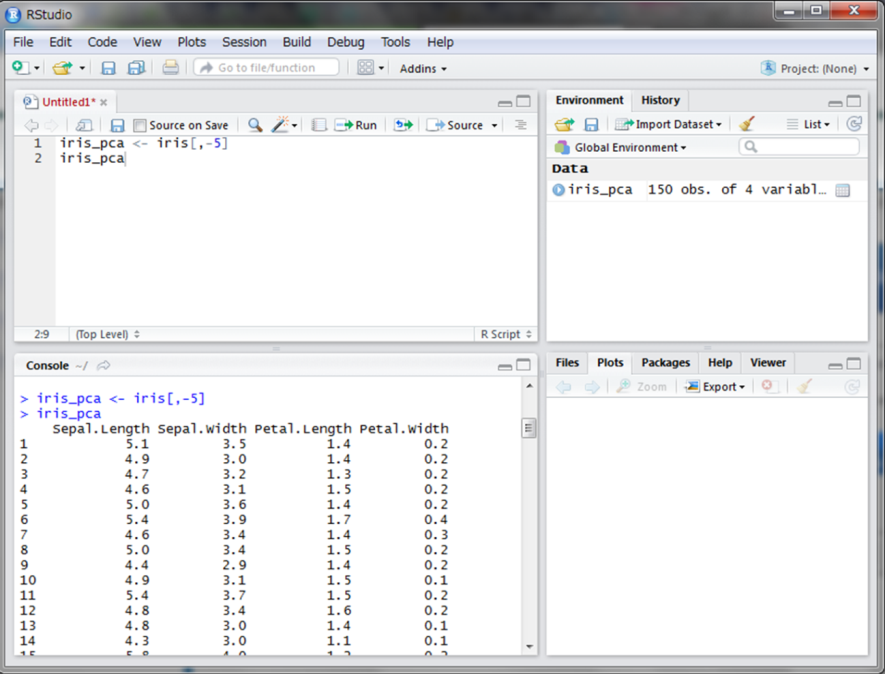
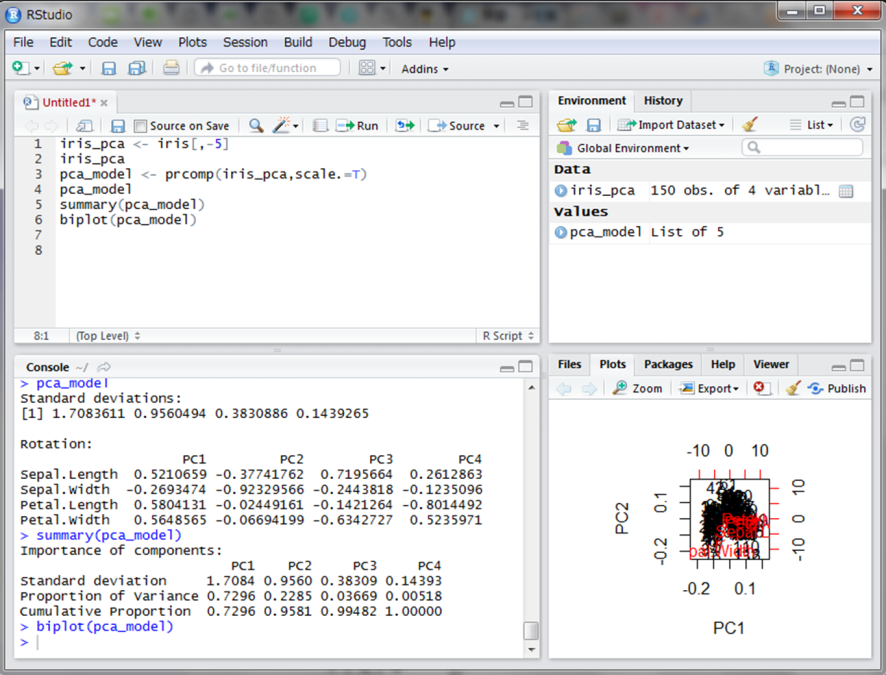
irisデータのうち、花の種類を表す5列目以外を抽出しiris_pcaに代入します。主成分分析はRのデフォルトにあるprcomp()関数を使用します。第一引数にデータを指定し、scale.引数にTRUE(Tで省略可)を指定します。pca_modelに代入し、結果を表示してみます。

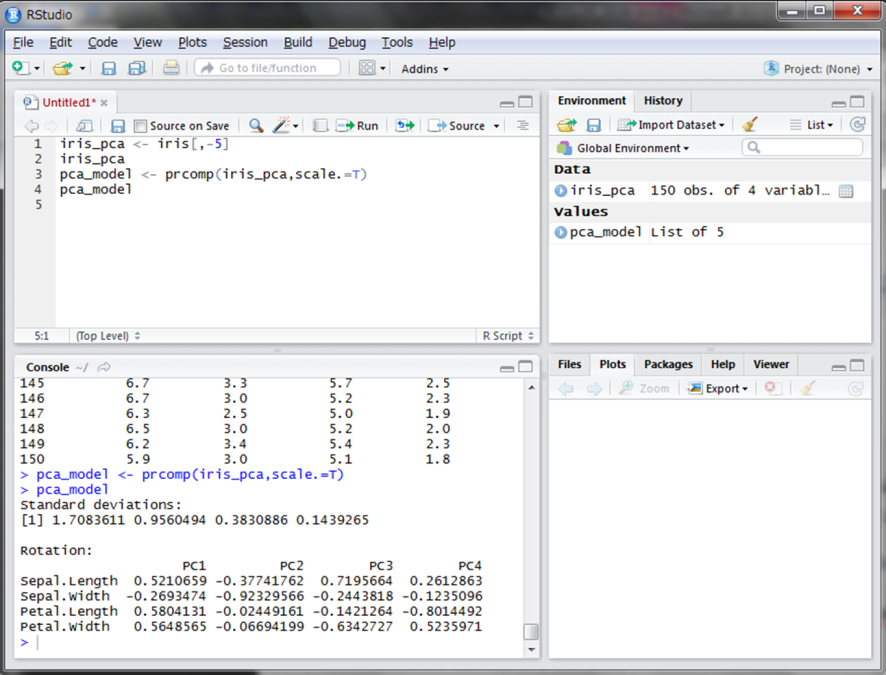
PC[数字]となっているのが、主成分の重みとなる部分です。上の数式のwに当たる数値です。では各主成分がどれだけの情報量を持っているのか表示してみましょう。summary()関数を使用します。

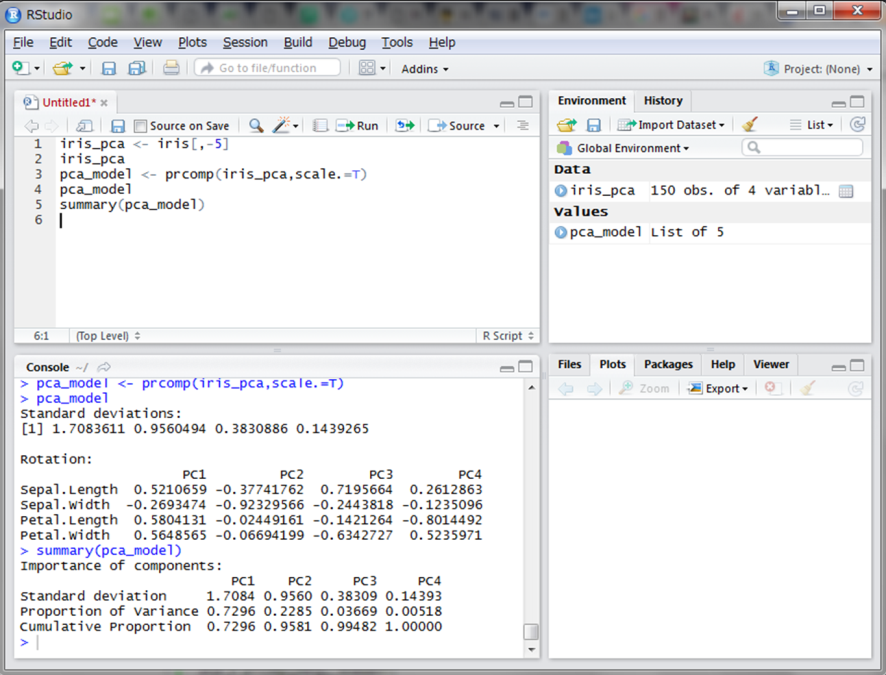
結果のCumulative Proportion(累積率)を見てみます。第1主成分までで約73%の情報量を保てているようです。また、第1主成分と第2主成分までで約96%まで情報量を再現できることを示しています。ここで、実際に第1主成分と第2主成分を用いて平面にプロットしてみましょう。biplot()関数を使うと便利です。

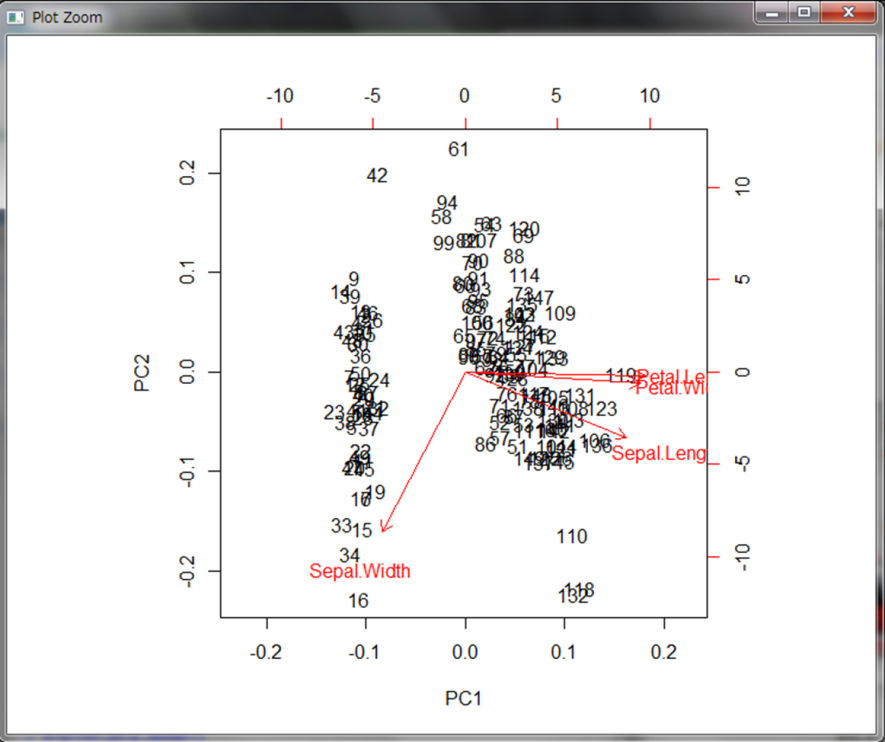
横軸が第1主成分、縦軸が第2主成分としたときのデータが順にプロットされています。
赤色で表示されている矢印と変数名の見方は、主成分に対してその変数がどれだけ寄与しているかを示しています。第1主成分では左に行くほどSepal.Widthが大きいデータが集まっていることを表しています。一方で右に行くほどPetal.LengthやPetal.Widthが大きいデータが集まっています。どちらも大きくないようなデータは中央に集まっています。また第2主成分は下に行くほどSepal.Widthが大きいデータが集まっています。ただし第1成分で左側にあるデータは大体Sepal.Widthが大きいデータが集まっているので、Sepal.Widthが大きいデータの中でも大小が分かれていると解釈されます。一方他の変数は第2主成分には大きく寄与していません。これらを考慮すると以下のような解釈ができます。

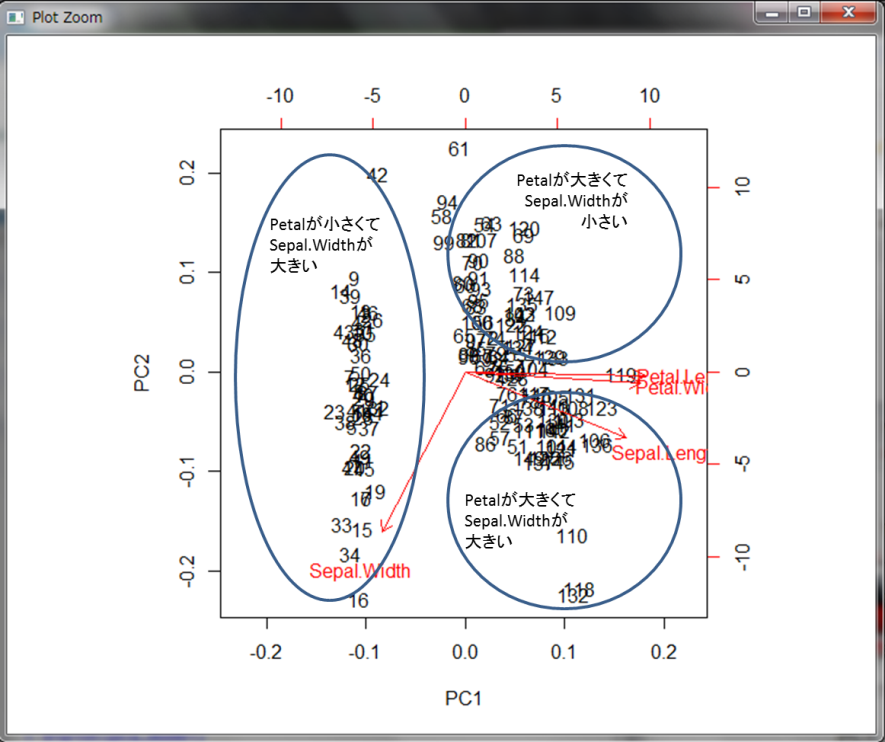
さて、今ラベルが数字になっているので、実際の花の種類で表してみます。花の名前を表示すると見にくいので、”○”、”×”、”□”で表示します。model_pcaの中に格納されているxという行列の行の名前を変更することでラベルを付けることができます。

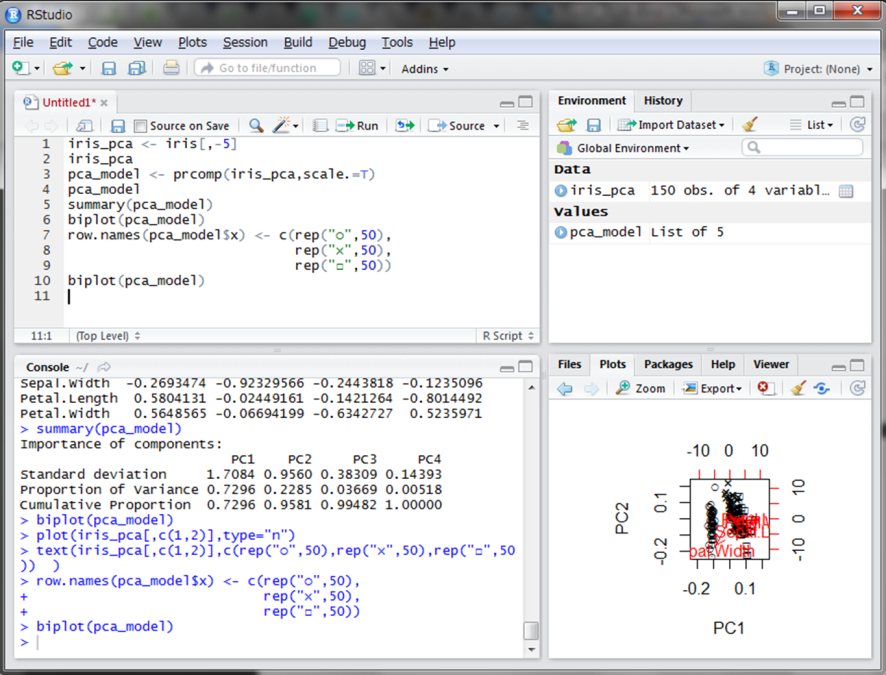
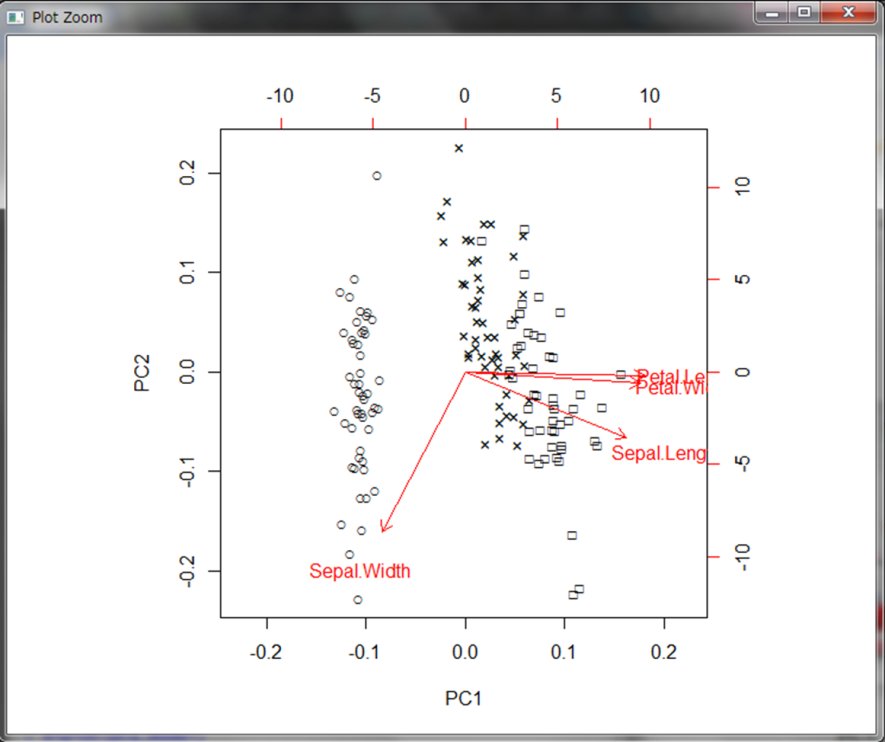
2つの主成分を用いてプロットした場合、3のクラスターに分かれていることが分かります。比較として、Sepal.LengthとSepal.Widthのみを使った場合の散布図を見てみましょう。なお、ここではtext()関数を使用することでプロットするデータにラベルを付けています。

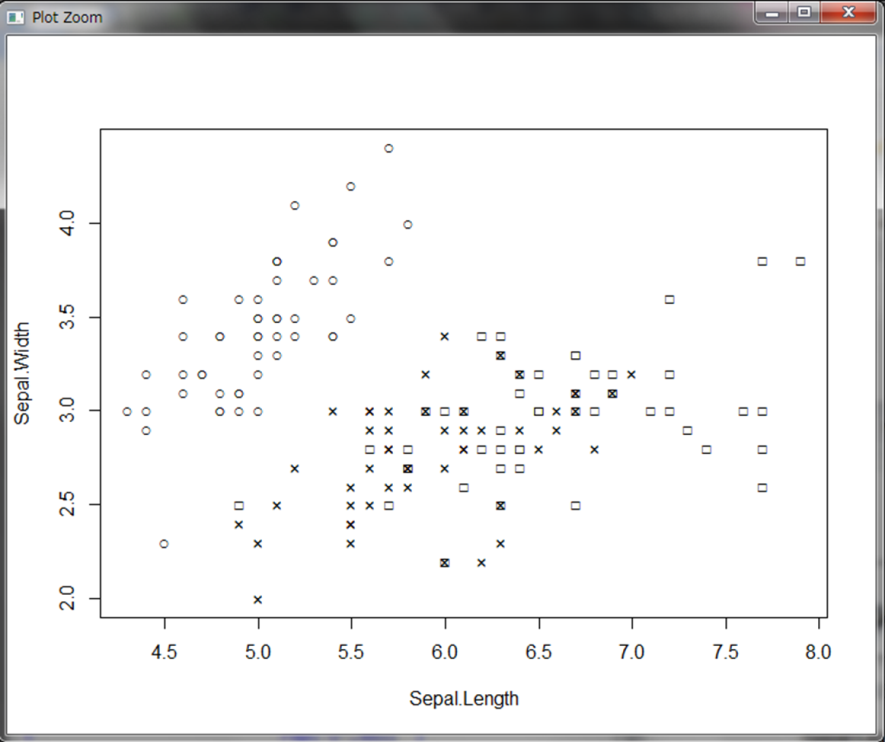
○の種類はSepal.Widthが大きい個体であり、主成分分析の結果と同じですね。一方×と□の種類はうまく分離できていないのが分かります。
このように、データがあるクラスターに分類されるような場合は、主成分を用いて平面にプロットし特徴を把握することができます。

都道府県別支出データで実践

次に、より高次元なデータを用いて実践してみましょう。
データは総務省統計局作成の平成26年全国消費実態調査より加工して作成しました。
こちらからダウンロードできます。

各都道府県別の支出費目における支出額を表すデータとなっています。早速取り込んで、主成分分析してみましょう。

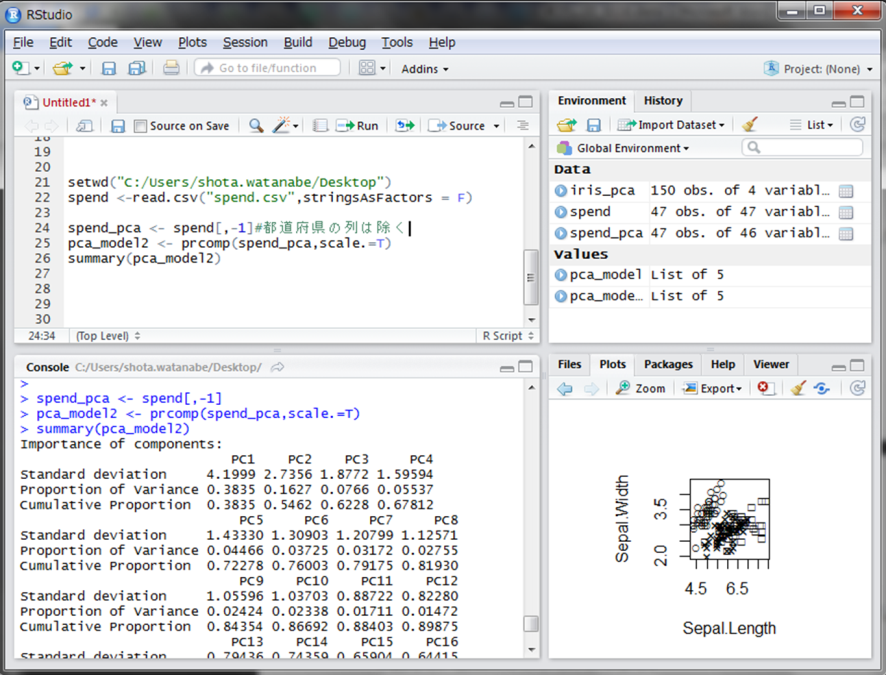
第2主成分までで約半分の情報量が欠失してしまいましたが、とりあえずbiplot()関数で描画してみます。

情報量が落ちているため正確な考察はできずあくまで個人的な意見に留まりますが、例えば左上の都道府県はどの変数からも離れているため、全体的に支出額がそれほど多くない都道府県のグループに属すと言えそうです。また右上の方に位置する都道府県は、「住居」「教育」「外食」「スポーツ」「旅行」に多くの支出があり、大都市の影響力がある都道府県と言えそうです。また、真ん中下ほどの都道府県は、住環境や移動手段などの変数が強いため、戸建てで車を所有している世帯が多い都道府県が集まっているようです。このように第2主成分だけでも大まかな考察や分類は可能で、どの都道府県同士が似ているのかが一目で把握することができます。