こんにちは。株式会社エル・ティー・エスの渡辺翔太です。
前回「データサイエンティストのお仕事とは?R基礎編」ではRの基本的なプログラミングについて学びました。
今回は、実際に手元にあるデータをRに取り込み、R上で扱ってみる回です。じっくり読み進めてみてください。
Rにデータを取り込む
データの準備
Rでデータ分析を行うためには、エクセルなどで保存しているデータをRに取り込む必要があります。しかし、デフォルト環境ではエクセル形式のファイルをRに取り込むことはできません。エクセル形式のファイルをRに取り込むには、CSV形式に変換する必要があります。
CSV形式とは、Comma-Separated Values形式の略で、データをカンマ(,)で区切ったテキストデータのことをいいます。
CSV形式で保存するには、「名前を付けて保存」画面の「ファイルの種類」から「CSV(カンマ区切り)(*.csv)」を選択して保存してください(メッセージが出る場合は、「はい」を選択してください)。また、Rに取り込む際にファイルの保存先が必要のため、保存先をきちんと把握しておいてください。慣れるまではデスクトップに保存するようにすると良いでしょう。
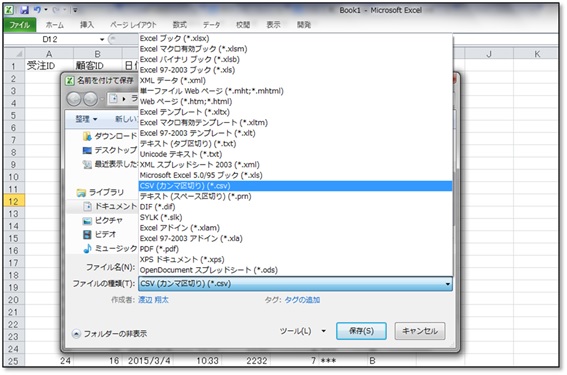
データをCSV形式で保存できれば、Rに取り込む準備が整いました。
今回、コラムで扱うCSV形式のデータを用意しました。実際に操作しながら読み進めてみてください。
データはこちらからダウンロードできます(右クリックからデスクトップに保存してください)。
作業ディレクトリの指定
Rには、作業ディレクトリという概念があります。作業ディレクトリとは、簡単に言えば「Rがアクセスできるフォルダ」のことです。作業ディレクトリ内にあるファイルは、簡単なコードでRに取り込むことができます。
今回は、先ほどのCSV形式で保存したファイル(以下、CSVファイル)をデスクトップに保存したので、作業ディレクトリにデスクトップを指定しましょう。作業ディレクトリの指定にはsetwd()関数という関数を使います。
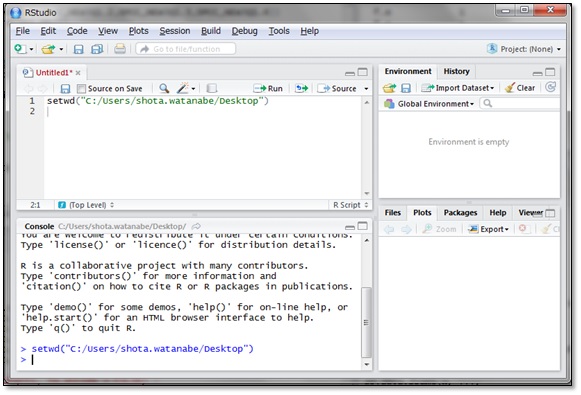
setwd()の引数にダブルクォーテーションでくくったフォルダのパス名を指定し、いつものようにCtrl+Enterで実行します。今回はデスクトップを指定するので、”C:/Users/ユーザー名/Desktop”という文字列を引数にしています。
実行結果の表示は特にありませんが、これで作業ディレクトリにデスクトップを指定することができました。
CSVファイルの読み込み
CSVファイルを取り込むにはread.csv()関数という関数を使います。引数にファイル名”Book1.csv”を文字列で指定し、その後ろに「, stringsAsfactors=FALSE」と記述して実行します。
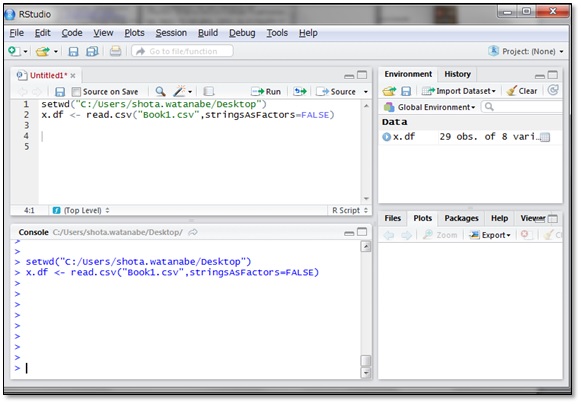
取り込んだCSVファイルはx.dfという変数に代入しています。CSVファイルを代入した変数はデータフレーム構造となります。データフレーム構造については前回のコラムで紹介していますのでご覧ください。
「stringsAsfactors=FALSE」というのは関数の処理に関するオプションの設定で、「因子型にしない」という指示を与えています。この指示を与えないと、文字列データが自動で因子型に変換されます。因子型とはデータ型のひとつで、文字列データに内部的に数値を与え、計算ができるようにしたものです。
しかし、因子型は少し扱いにくいので、ここでは「因子型にしない」と明示的に指定しています。
以上で外部のデータをRに取り込み、x.dfという変数に代入することができました。
取り込んだデータを用いて簡単なデータ分析を行う
データの確認
str()関数を用いると、データフレームの各列がどのようなデータ型なのか表示することができます。
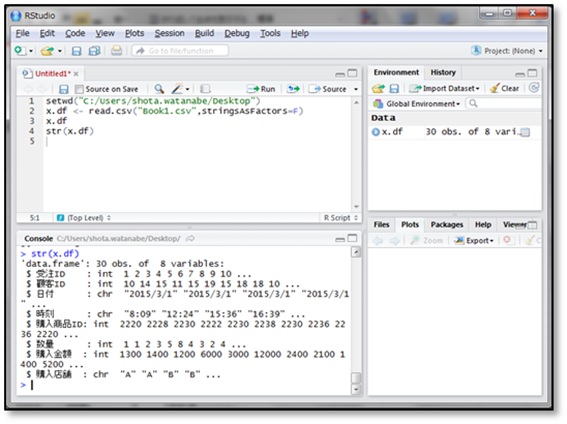
ドルマーク($)の後ろにあるのがデータの列名で、その右の英字3文字がデータの型を表します。
- chr:文字列
- cplx:複素数型
- num:実数型
- int:整数型
- logi:理論値型
そして、各列の具体的な値がいくつか表示されます。
基本統計量
複数の数値データの特徴を表す数値のことを基本統計量といいます。よく知られているものだと、平均が挙げられます。その他にも中央値や最頻値、分散や標準偏差なども基本統計量の一部です。基本統計量について次の表にまとめました。

Rにデフォルトで存在する分散と標準偏差の関数は、不偏分散および不偏標準偏差を出力します。ご注意ください。
実際にx.dfにある購入金額について上記の基本統計量を算出してみましょう。
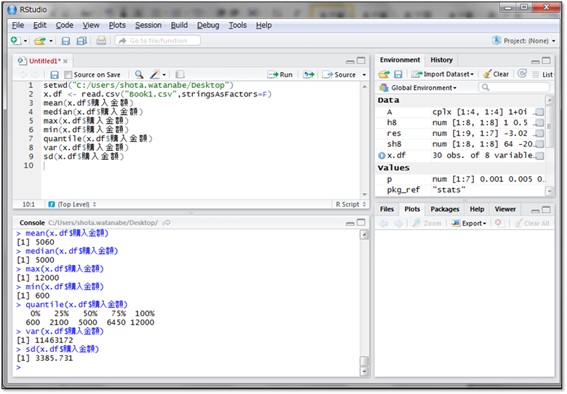
購入金額の平均は5,060円、中央値は5,000円、最大値は12,000円、最小値は600円、第1四分位点(データ数の1/4番目の四分位点)は2,100円、第3四分位点(データ数の3/4番目の四分位点)は6,450円、分散は11,463,172円2、標準偏差は3,385.731円と分かりました。
ここから分かることとしては、
- ①平均と中央値が近いことから、平均を中心に左右均等にデータがありそう
- ②最大値と最小値の差が大きいことから、データの取りうる値が幅広そう
- ③データの最小値から最大値に向かって1/4進んだ値よりも第1四分位点の方が小さい(600+(12000-600)÷4=3450>2100)ことから、データのばらつきが大きそう
などが挙げられます。
標準偏差とは
x.dfの購入金額にはなんとなくばらつきが大きそうであることが分かりました。実際にデータのばらつきを表す標準偏差を見てみることにします。
ここで、標準偏差の特徴をひとつ紹介します。それは、平均±標準偏差の範囲に全データ数の約68%のデータが含まれるというものです。
データがばらついていると、68%のデータを範囲内に収めるには、標準偏差は大きくなければなりません。逆に平均付近にデータが集まっているような場合では、小さな範囲で68%のデータを収めることができるので標準偏差は小さくなります。
今回の例でみると、30件のデータの68%は20件ですので、5,060円±3,386円の範囲に20件のデータが含まれると予想されます。実際にカウントしてみましょう。
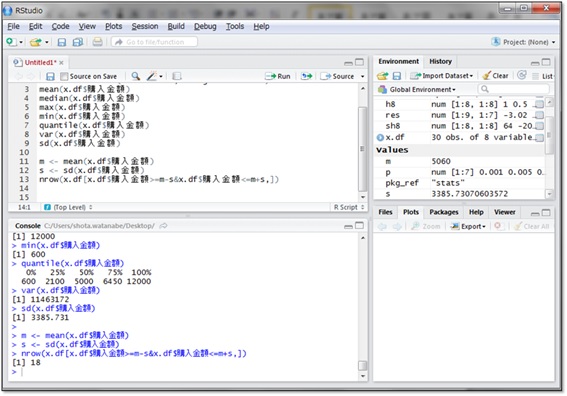
まず、変数mに平均を、変数sに標準偏差を代入しています。
nrow()関数は、データフレームの行数をカウントする関数です。購入金額が「平均-標準偏差」以上という条件と、「平均+標準偏差」以下という条件の両方を満たすデータをx.dfから抽出し、nrow()関数の引数にしています。複数の条件をすべて満たすものを指定したい場合は、条件と条件を”&”でつなぎます。
指定した条件を満たすデータの数は18個ということが分かりました。想定していた20件にやや
満たないですが、データ数が少ない場合や偏りがある場合には、このようにずれが生じることがあります。
この標準偏差の考え方は、工場で生産される部品の品質管理などにも用いられています。部品の重さの標準偏差を定期的に算出することで、たとえば標準偏差が通常時よりも大きいときには、部品の重さがばらつき始めたということに気付くことができます。標準偏差を定期的に観測することで異常に早めに気付くことができ、早急な対応が可能となります。
一方で、部品の重さが全体的に増加または減少した場合、標準偏差だけ見ていても異常に気付くことはできません。その時には平均と標準偏差の両方を見る必要があります。平均と標準偏差を用いることで現在の状態が正常なのか異常なのかを統計的に正しい理論で決めることができます。このお話は次の回で紹介したいと思います。
それでは第3回のコラムはここまでです。次回をお楽しみに!
アサインナビでは、データサイエンスに関するセミナーを随時開催しております。
過去には、データサイエンティストの知識を習得するための実践塾や、特別講師を招いてのセミナーなどを開催しております。
過去の様子はこちらからご確認いただけます。
▼データサイエンティスト実践塾▼
第1回データサイエンティスト実践塾を修了しました!
▼データサイエンスの現状と未来▼
シリコンバレーに学ぶ、日本のデータサイエンスの現状と未来 ~これからのデータドリブンな時代に本当に必要なこと~を開催しました







