こんにちは。株式会社エル・ティー・エスの渡辺翔太です。
前回、確率分布についての概要と代表的な確率分布について説明しました。今回は前回記載した代表的な確率分布の具体的な性質を、Rを用いて見ていきたいと思います。
確率分布に従う乱数の発生
まずは、確率分布に従う乱数を発生させてみたいと思います。どのような確率分布から、どのような値が実際に発生するのかを目で見ることができるので、イメージが湧きやすいと思います。確率分布でいうところの、xの値をシミュレーションするイメージです。
前回、確率分布には離散確率分布と連続確率分布の二つがあると説明しました。
離散確率分布からは二項分布とポワソン分布、連続確率分布からは一様分布と正規分布を取り上げてRで見ていきたいと思います。
・二項分布の乱数発生
二項分布は「成功確率pの試行をn回行うとき、成功する回数がx回であるときの確率」を表す確率分布で、次の確率密度関数を持ちます。
乱数を発生させるときには、あらかじめ試行を何回行なうかと、成功する確率pを決めておく必要があります。
3割打者が10打席で何回ヒットを出せるか、シミュレーションしてみましょう。
試行の回数は10、成功確率は0.3です。
Rで二項分布の乱数を発生させるには、rbinom()関数を使用します。
rbinom()関数の引数には、n、size、probというものがあります。nは発生させる乱数の個数、sizeは試行回数、probは成功確率です。nが試行回数ではないので注意してください。まずは1個だけ発生させてみましょう。
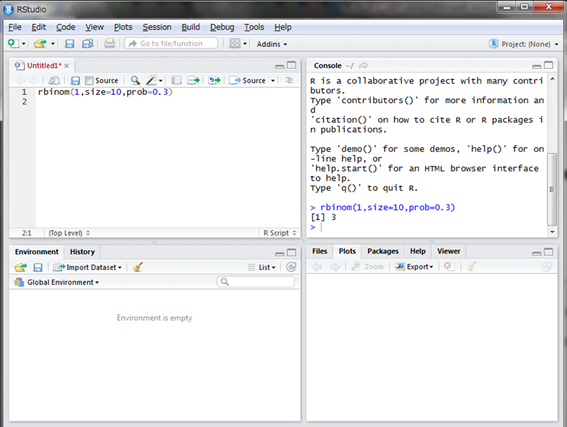
3が出ましたね。3割打者なので妥当な乱数ではないでしょうか。もう一度発生させてみます。
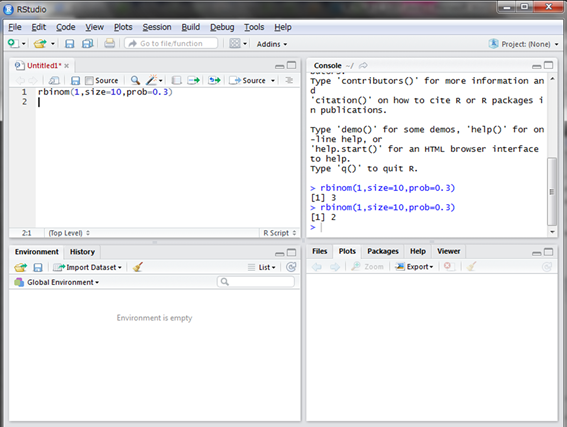
次は2が出ました。不調な時は2回しか打てない時もあります。
選手には過酷ですが、1試合10打席に必ず立ってもらう試合を1000試合してもらいましょう。つまり、1000個の乱数を発生させてみます。
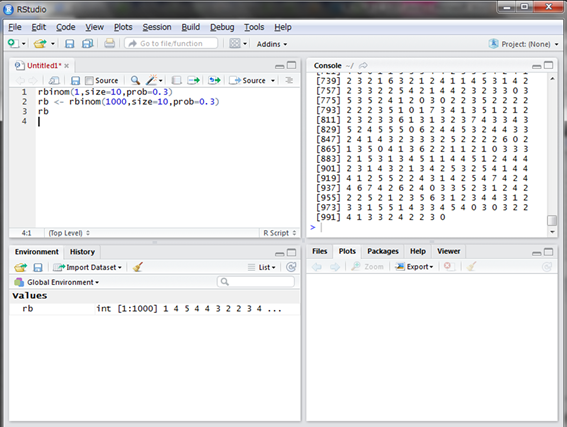
200個くらいの乱数が表示されていますが、10打席中ヒットなしの場合もあれば、7回ヒットという好成績の場合もありますね。
実際にどのような乱数がどの程度発生したかをグラフで見てみましょう。
table()関数で集計し、barplot()関数で棒グラフにします。
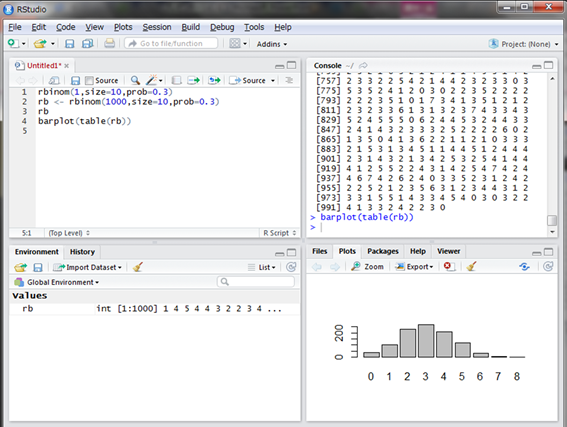
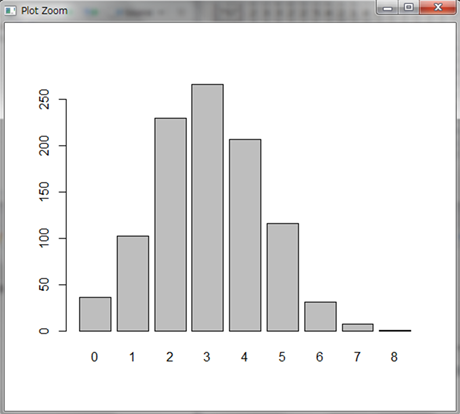
1000試合した結果、3回ヒットが最も多いですね。3割打者というだけありました。また、3割打者といってもヒット2回やヒット4回はよく起こることも分かります。一方で、8回もヒットを出した奇跡の試合もあったようです。このような奇跡はいつも起こるわけではないので、読者の皆さんの中には8回ヒットがなかったかもしれません。もしくは極まれに9回ヒットや10回ヒットの場合もあるでしょう。
・ポアソン分布の乱数発生
ポワソン分布は「一定期間に0回、1回、2回、…と数えられる事象に対して、平均λ回発生する場合に、その期間にk回発生する確率」を表す確率分布です。その確率密度関数は次のように表されます。
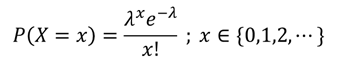
ここでは例えば、1時間に平均5通のメールが来ることが経験的に分かっているときに、今から1時間の間に何通メールが来るかシミュレーションしてみましょう。ポワソン分布に従う乱数はrpois()関数を使います。その引数は乱数の個数nと、平均発生回数lambdaです。
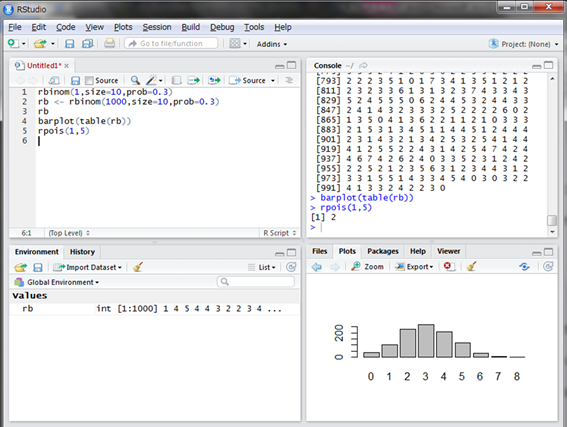
今回は2が出ました。2通しか来ないと嬉しいような寂しいような気がしますね。次に1000回シミュレーションをして1000個の乱数を発生させてみましょう。
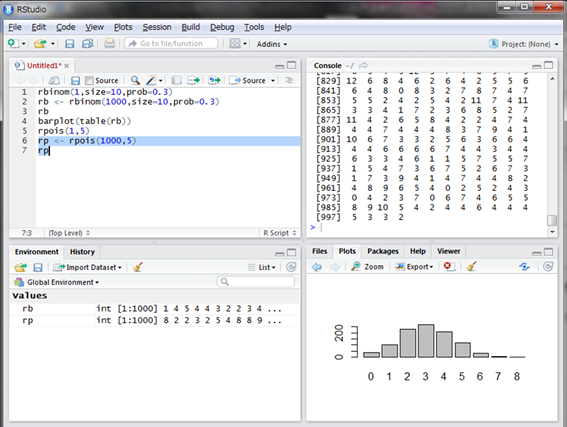
平均5通といっても0通や12通なども見られますね。同様に結果をグラフにしてみましょう。
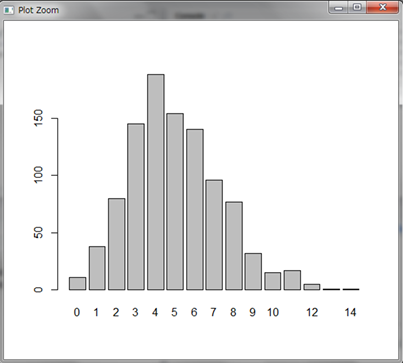
1時間に平均5通メールが来るのに、結果として4通が最も多いシミュレーションとなりました。見てみると、6通以上来る場合もかなり多く、特に10通以上の結果も割と発生しています。最もよくあるメールの件数は4通だけど、メールが多く来る場合も割と発生するから平均すると5通になる、ということです。平均5通くらいだろうと思っていたら10通以上メールが来てしまい大変な思いをしたという経験、ありませんか?
次は連続確率分布に移ります。一様分布と正規分布ですね。
・一様分布の乱数発生
一様分布は、確率変数Xの取りうる値xについて、同じ長さの任意の範囲にあるxであれば同じ確率で発生する場合の確率分布です。
確率密度関数は次の式で表されます。
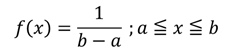
Rでの発生方法はrunif()関数を使います。引数は個数n、範囲の最小値min、範囲の最大値maxです。デフォルトではmin=0、max=1に設定されています。ここではデフォルトのままで0から1の範囲から任意の数値を発生させてみます。
0.899575という値が発生しました。同じように1000個の乱数を発生させ、グラフにしてみましょう。ただし、発生する値は1個2個と数えられるものではないので、集計せずにそのままhist()関数でヒストグラムにします。
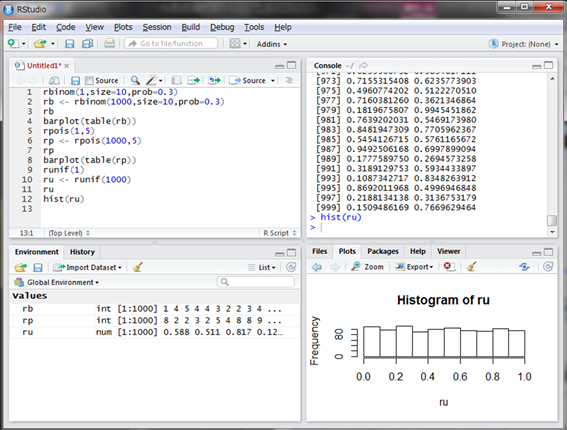
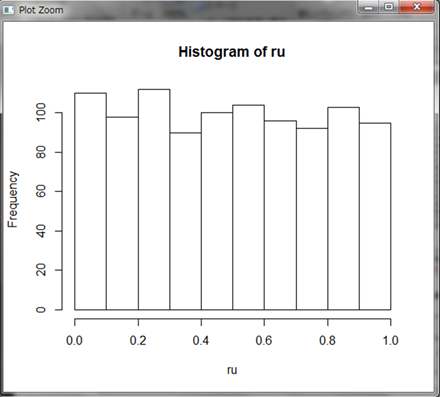
多少のバラつきは見られますが、およそどの範囲に含まれる乱数の個数も同じような数になっています(乱数の発生個数を大きくするとこのバラつきは小さくなっていきます)。そして、どのような数値であっても指定した範囲であれば等しい確率で発生することが分かります。
・正規分布の乱数発生
正規分布とは、平均値付近の値を良く取り、平均値を中心に左右対称となる値は同程度の確率で発生するような分布を表します。統計学では最も基本的な確率分布です。
確率密度関数は次の式で表され、平均パラメータμと分散パラメータσ2が存在します。
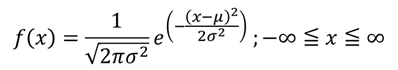
高校受験の時によく耳にした偏差値は、試験の得点が正規分布に従うと仮定したときに、試験の平均を50、標準偏差を10に変換した時の試験の得点を表します。例えば自分の得点が90点で、そのとき全体の試験の平均が60、標準偏差が15だったとします。すると、偏差値は70になります。もし全体の試験の平均が60でも標準偏差が30だとしたら、同じ90点でも偏差値は60となります。計算式は調べれば出てきますので詳細は割愛します。
それでは平均50、標準偏差10の正規分布に従う乱数を発生させてみましょう。Rではrnorm()関数を使用します。引数は個数n、平均mean、標準偏差sdです。デフォルトでは平均mean=0、標準偏差sd=1で設定されています。
ここでの想定は、無限にいる学生から1人選んで、その学生のある試験の偏差値を調べるイメージです。
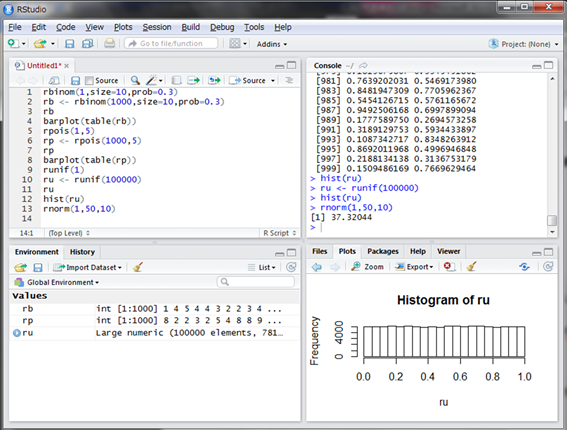
偏差値37の学生が選ばれました。学生の学力云々は置いておいて、この偏差値の学生は実は結構います。このことは10000人選んでヒストグラムを見れば分かります。実際にシミュレーションしてみましょう。
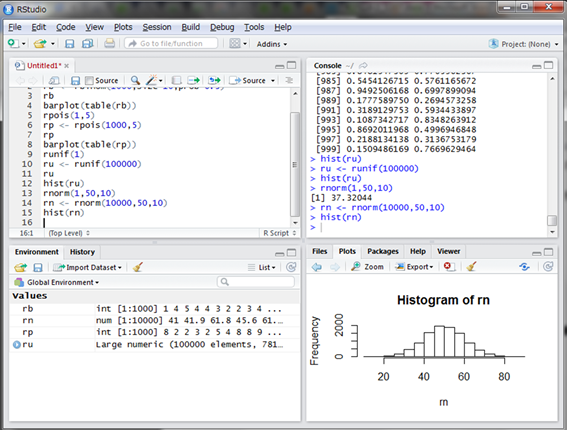
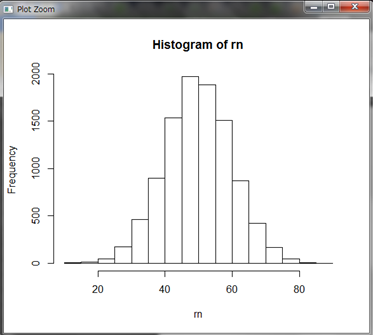
偏差値37付近の学生は10000人中1000人弱はいそうですね。
また、平均50の付近にデータが集中していることも分かります。ちなみに、平均±標準偏差、すなわち偏差値40~60に含まれる学生の割合はおよそ68%となります。同様に偏差値30~70ではおよそ95%、20~80ではおよそ99.5%となります。そのことをシミュレーションの結果から確認してみましょう。
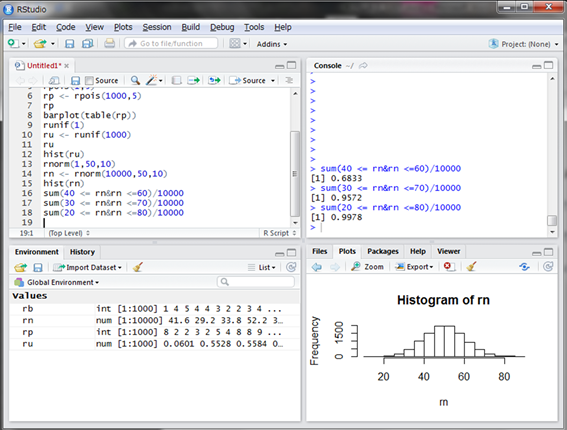
想定どおりの結果となりました。
つまり、偏差値が40~60となる確率は約68%と言えます。次の章ではこれを厳密に計算し、かつどのような範囲の確率も算出します。
確率分布から確率の計算(正規分布のみ)
さきほど正規分布に従う乱数を発生させ、ヒストグラムを描きました。そして、乱数がある範囲に含まれる割合を算出しました。しかし、乱数として発生させたものなので厳密な確率ではないですし、毎回シミュレーションするのも大変です。そこで、Rを用いて正規分布に従うデータがある範囲に含まれる確率を計算しましょう。
前回のおさらいですが、正規分布の確率密度関数は次の式で与えられます。
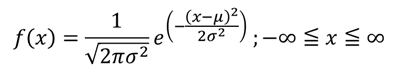
そして、ある範囲の確率は次の計算で求めることができます。
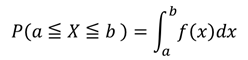
つまり、確率を求めるためには積分をする必要があります。
まずRで確率密度関数f(x)のグラフを描いてみましょう。Rではf(x)はdnorm()関数となります。dnorm()関数も引数に平均meanと標準偏差sdが必要となります(デフォルトはmean=0、sd=1)。そしてある関数のグラフを描くcurve()関数と組み合わせます。from引数とto引数でx軸の範囲を指定します。
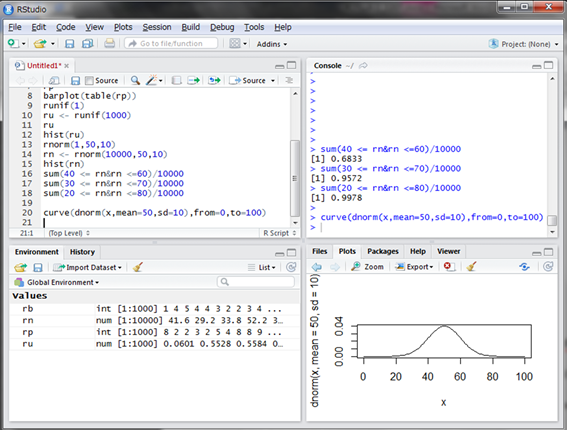
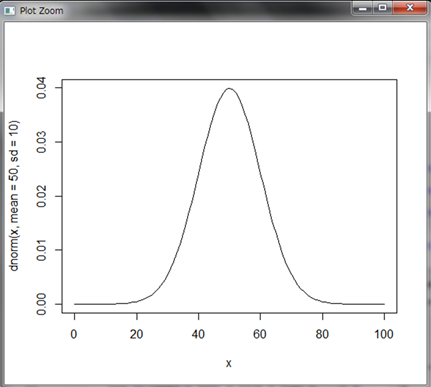
ヒストグラムの形状と同じような形になっています。xが0や100の時には0にとても近い値ですが0より少し大きい値になります。xがどんどん小さくなっても、またどんどん大きくなっても0に限りなく近づきますが0になることはありません。
そして、この確率密度関数のグラフと確率の関係ですが、式では
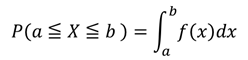
こうですが、グラフにするとこうなります。
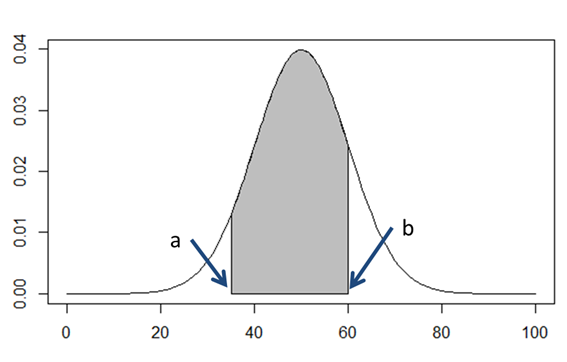
つまり確率密度関数のグラフのある範囲における面積が、その範囲にデータが発生する確率を表しているのです。
さて、Rには確率密度関数から確率を求めるpnorm()関数が用意されています。しかし、この関数は下図の面積しか求めることはできません。
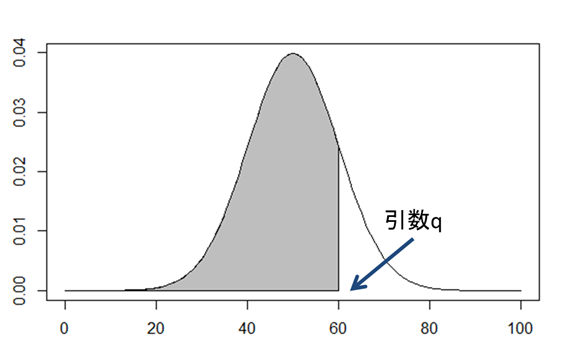
つまり、pnorm()関数の引数qで指定した値以下のデータが発生する確率が計算されます。ここではq=60にしています。
ある2つの値で囲まれた範囲の確率、例えば40~60の範囲の確率を求めるには、pnorm()関数を2つ用意し、それぞれの引き算で求めることになります。
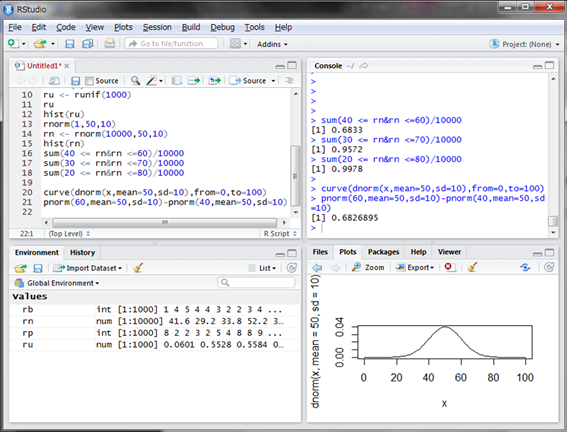
よって、偏差値40~60の範囲にデータが入る確率は68.26895%ということが計算されました。
ちなみに、偏差値90以上となる確率はどのように計算すればよいでしょうか。
実はpnorm()関数の引数にlower.tailというものがあり、通常TRUE値となっています。これをFALSEに変更すると引数q以上の確率を計算してくれます。
図でいうと次の色つきの面積です。
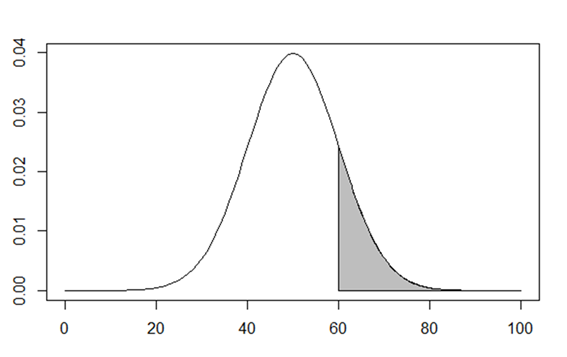
先ほどの面積と逆方向の面積ですね。なので偏差値90以上の学生が選ばれる確率は次のようになります。
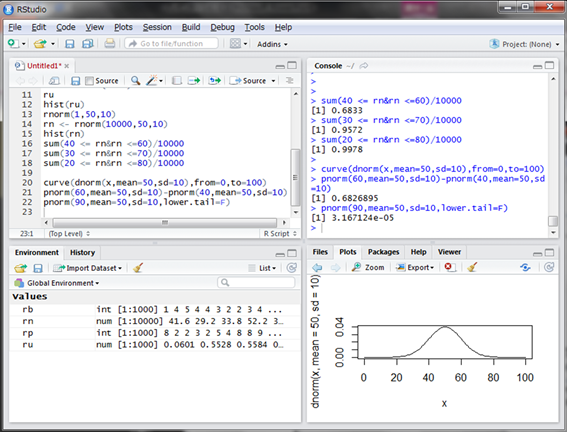
3.167124e-05という値は0.00003167124ですから、約0.003%ですね10万人に3人の割合しかいません。今年のセンター試験受験者数が56万人ですから、トップ17人は偏差値が90以上のつわものと言えます。
ちなみに、確率からデータの範囲を求めることもできます。qnorm()関数を使用します。例えば上位10%に入るのに必要な偏差値は次のように計算します。
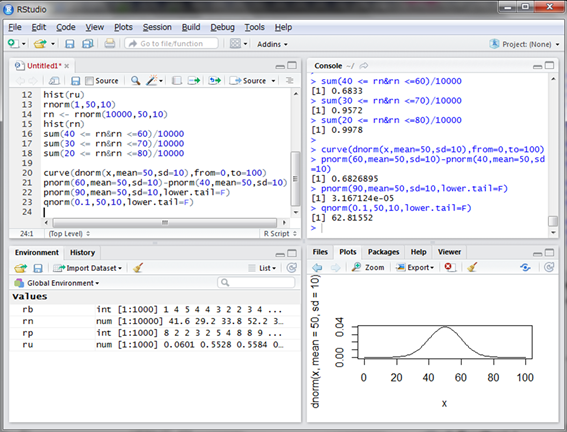
第一引数に確率を与えます。今回は上位10%なのでlower.tailをF(FALSEの略)にしています。偏差値が62.8以上あれば上位10%には入れるということですね。
いかがでしたでしょうか。確率分布の話は少し数学的な話も多かったですが、これからデータ分析を進める上では重要な概念となってきます。世の中には様々な確率分布が存在します。それは、それだけ世の中の事象が複雑であるということに他なりません。今回は基本的なものだけを取り上げましたが、これから先他にどんな確率分布があり、どのようなデータの分布を表しているか探してみると面白いと思います。
アサインナビでは、データサイエンスに関するセミナーを随時開催しております。
過去には、データサイエンティストの知識を習得するための実践塾や、特別講師を招いてのセミナーなどを開催しております。
過去の様子はこちらからご確認いただけます。
▼データサイエンティスト実践塾▼
第1回データサイエンティスト実践塾を修了しました!
▼データサイエンスの現状と未来▼
シリコンバレーに学ぶ、日本のデータサイエンスの現状と未来 ~これからのデータドリブンな時代に本当に必要なこと~を開催しました







