データサイエンティストのお仕事とは？【第11回前半】機械学習編その3 ナイーブベイズ分類器（その1）

こんにちは。株式会社エル・ティー・エスの渡辺翔太です。
今回は機械学習編の続きです。機械学習の手法の1つであるナイーブベイズ分類器について説明していきます。文書の分類に用いられます。
ナイーブという言葉は、日本では「繊細な」という意味で使用されますが、本来の意味は「単純」「素朴」という意味です。この機械学習法のどのあたりが単純なのかも説明していきたいと思います。

■目次■

ベイズの定理
ナイーブベイズ分類器とは

ベイズの定理

ナイーブベイズ分類器の理論はベイズの定理から出発します。ベイズの定理を理解するために、まずは「条件付き確率」を考えます。

条件付き確率とは、ある条件の下で事象が起こる確率のことを指します。
例えば、男女比が40%：60%の集団があり、眼鏡を掛けている人の割合は男性が30%、女性が25%だとします。この集団から1人無作為に選んだ時、眼鏡を掛けている確率を考えます。
集団が100人とすると、男性が40人、女性が60人です。その中で眼鏡を掛けている人は男性が12人、女性が15人です。合計27人なので、100人中1人選んだ時に眼鏡を掛けている確率は27%となります。
さて、無作為に選んだ1人が眼鏡を掛けている事象を「眼鏡」とし、その確率をP(眼鏡)とおきます。さきほどの計算からP(眼鏡)=0.27です。
また、性別が男性という事象を「男性」、性別が女性という事象を「女性」と表します。P(男性)=0.4、P(女性)=0.6です。

では、「選ばれた人の性別が男性という条件の下で眼鏡を掛けている」という事象を考えましょう。
男性のうち30%が眼鏡を掛けていることから、この事象が起こる確率は0.3です。これを条件付き確率と呼び、P(眼鏡|男性)=0.3と表します。同様にP(眼鏡|女性)=0.25です。

さらに、「選ばれた人の性別が男性で、かつ眼鏡を掛けている」という事象を考えます。これは同時確率と言って、P(眼鏡,男性)と表記します。同様に性別が女性で、かつ眼鏡を掛けている場合はP(眼鏡,女性)となります。このとき、コンマ(,)の前後の順序に意味はなく、入れ替えても同じ意味です。
単に眼鏡を掛けている人は、「男性で眼鏡を掛けている人」＋「女性で眼鏡を掛けている人」なので、P(眼鏡)= P(眼鏡,男性)+ P(眼鏡,女性)が成立します。

さらにP(眼鏡,男性)=P(男性)×P(眼鏡|男性)、P(眼鏡,女性)=P(女性)×P(眼鏡|女性)が成り立ちます。
よって、P(眼鏡)=P(男性)×P(眼鏡|男性)+P(女性)×P(眼鏡|女性)が成り立ちます。実際、0.27=0.4×0.3+0.6×0.25となっています。

ここで、「選ばれた人が眼鏡を掛けているという条件の下で、その人が男性である」確率を考えてみましょう。
これはP(男性|眼鏡)と表されます。眼鏡を掛けている人は全体で27人いて、そのうち男性は12人なのでP(男性|眼鏡)=12/27=4/9です。これにP(眼鏡)=0.27を掛けるとP(男性|眼鏡)×P(眼鏡)=0.12となり、P(眼鏡,男性)と一致します。

さらに、P(眼鏡)=P(男性)×P(眼鏡|男性)+P(女性)×P(眼鏡|女性)が成り立つことから、P(男性|眼鏡)=P(眼鏡|男性)×P(男性)/{P(男性)×P(眼鏡|男性)+P(女性)×P(眼鏡|女性)}となり、最初に出てきた確率のみで計算することができます。

実際、4/9=0.3×0.4/(0.4×0.3+0.6×0.25)が成立しています。
一般化すると次のようになります。この式のことをベイズの定理と呼びます。

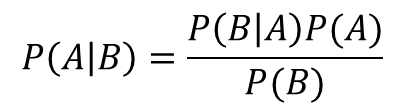
また、Aが互いに排反な事象A1,A2,…,Anに分解される場合、

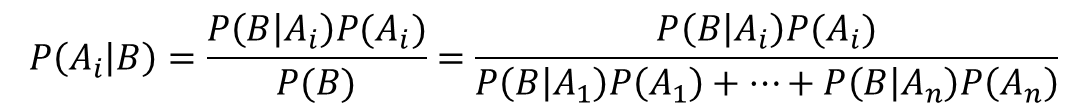
となります。これはA1が男性、A2が女性、Bが眼鏡のような感じですね。

ナイーブベイズ分類器とは

さて、ナイーブベイズ分類器の話に進みます。多次元データXからカテゴリYを分類することを考えます。例えば、Xはある記事に出現する単語たちの頻度で、Yは記事の分類（政治、スポーツなど）だとします。

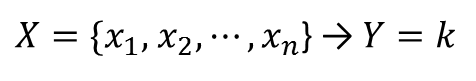
データXが得られたときに、それがkというカテゴリに分類される確率は、条件付き確率を用いて次のように表されます。

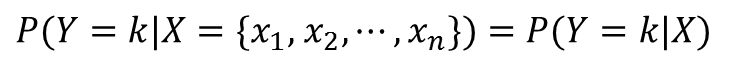
ベイズの定理を用いると次のように変形できます。

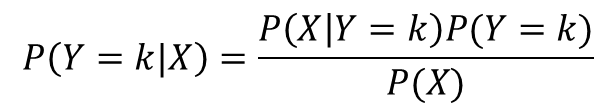
この確率を各カテゴリkについて計算し、確率が最も高いカテゴリkに分類ことを考えます。すなわち、データXが得られたときに分類される確率が最も高いカテゴリに分類するアルゴリズムを分類器を考えます。
ここで、分母のP(X)はkに依存しない値なので、計算する必要はありません。P(X|Y=k)とP(Y=k)を過去のデータから計算することができればよいことがわかります。

P(Y=k)は、過去の全データ数のうちカテゴリkに分類されたデータの割合を利用することが多いです。しかし、カテゴリごとにデータ数が大きく異なる場合はデータ数が多いカテゴリほど確率が高くなり、その値に引きずられます。このような場合はP(Y=k)=1として一定にします。
P(X|Y=k)は、カテゴリkという条件の下、Xというデータが得られる確率です。記事の場合は、カテゴリkという条件の下で記事X（正確には単語たちの頻度）が得られる確率です。しかし、同じ単語群で同じ頻度となる確率はほぼゼロです。そこで、P(X|Y=k)の計算に「ナイーブ」な工夫をします。

通常、Xに含まれる要素は互いに独立ではありません。記事の場合、”サッカー”という単語があれば”シュート”という単語も高い確率で出てくるでしょう。このように要素間の相関があるのが普通です。しかし、この要素間に独立性を仮定し単純化することがナイーブベイズのナイーブたる所以です。
そうするとP(X|Y=k)は次のように計算されます。

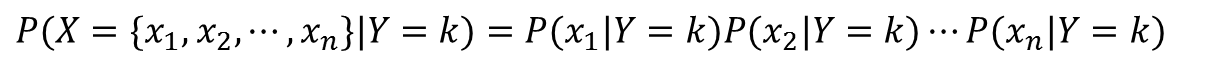
こうすることで、カテゴリがkのときの各要素に関する確率の積で表すことができました。
あとはカテゴリごとに各要素の確率を求めるだけです。これは要素xの性質によって変わりますが、連続数値を取る場合は正規分布の確率密度関数、xも何かのカテゴリ変数である場合はその割合、単語の頻度などの場合は多項分布から計算するのが一般的です。

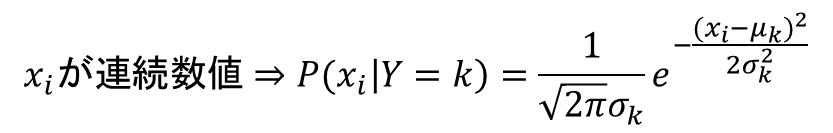
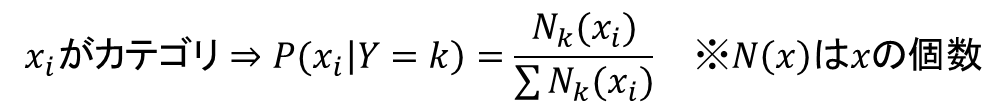
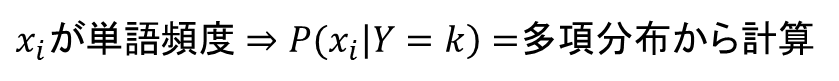
これらの学習データから、各kごとに計算します。
最後に、

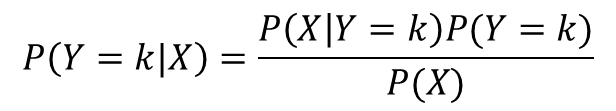
に当てはめるとナイーブベイズ分類器の完成です。

その後新しいデータ

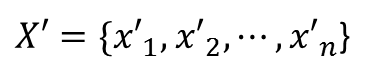
が得られたとします。これがナイーブベイズ分類器どのカテゴリに分類されるか計算します。
書くkごとに次の計算をします。

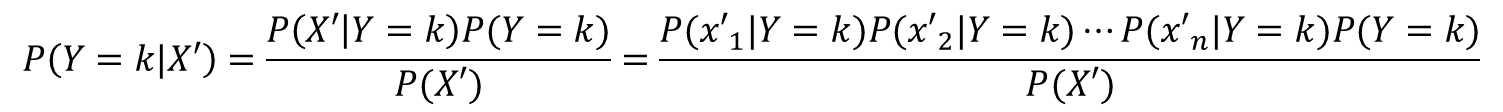
P(X’)はkに依存せず、またどのkにも分母に出現するので、除外してもP(Y=k|X’)が最大となるkが変わりません。
ですから、各kについて次の計算を行い、

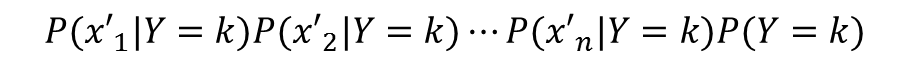
この値が最大となるkに分類します。
これでナイーブベイズ分類器が完成しました。