こんにちは。株式会社エル・ティー・エスの渡辺翔太です。
データサイエンティストの仕事内容を紹介するコラムの第4回目となる今回は、仮説検定についてお話しします。分量が多いので、2回のコラムに分けてお送りします。
前半では仮説検定の概要について説明し、後半では実際にRを用いて仮説検定を行います。一気に統計っぽい内容に入っていきますので、少しずつ読み進めてください。
仮説検定とは
仮説検定の話に進む前に、「検定」という言葉について考えてみましょう。
普段よく耳にする「検定」とは、漢字検定や日本語検定などの検定試験のことを指しているのではないでしょうか。これらの試験は、「受験者に漢字や日本語の能力があるかどうか」という命題を所定の方法に基づいて検査し、ある基準を基に合格や不合格を決めるものです。
統計学における仮説検定も同様に、検査されるべき命題があり、検査するための所定の方法があり、ある基準が設けられ、その基準をもとに合格か不合格のどちらかが決まるものとなっています。
まずはこれらの手順に簡単に説明したいと思います。
仮説検定の手順1:仮説を立てる
「受験者に漢字や日本語の能力があるかどうか」という命題は言い換えると、「受験者に漢字や日本語の能力がある」という仮説を立てていることと同じことです。その仮説が正しい場合は合格、間違っている場合は不合格となります。
統計学の仮説検定では、この仮説の立て方に注意しなければなりません。
たとえば「今月の平均客単価は前年同月に比べ低い」という命題は、仮説ではありません。今月と前年同月の平均客単価を単純に比較すればどちらが低いかは明らかです。
前年10,000円だった客単価が9,990円になった場合も、8,000円になった場合も、ともに「低い」と結論付けることができます。
仮説になるのは、「その差が偶然によるものなのか、それとも何らかの要因で生じた差なのかどうか」という命題です。つまり統計学における仮説検定は、すでに得られたデータが示す事実に対して、その解釈を助けるものです。
例えば、前年10,000円だった客単価が9,990円になった場合、これが偶然でない差であったとしても、もしその程度の差を問題にしないのであればそもそも仮説検定を行う必要がありません。
また、偶然10円の差が生じていたとしても、その差が経営上大きな問題であり何とかしないといけない場合は、仮説検定の結果に関わらずアクションが求められます。
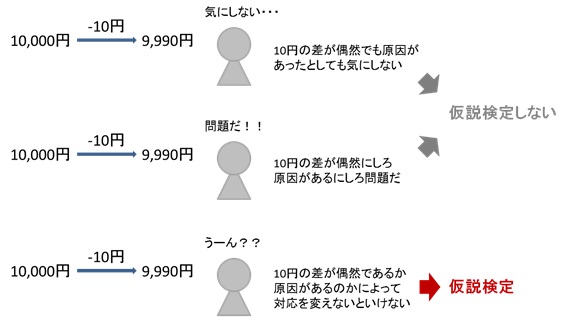
10円の差が偶然かどうかでその後の対応を判断したい場合に仮説検定は有効です。その場合、次の仮説を立てることになります。
仮説:「今月の平均客単価は前年同月に比べ偶然でないほど低い」
このように「差がある」という仮説を統計学では対立仮説と呼びます。これと反対に「差がない」という仮説のことを帰無仮説と呼びます。
- 対立仮説:「今月の平均客単価は前年同月に比べ偶然でないほど低い」
- 帰無仮説:「今月の平均客単価は前年同月に比べ差がない(差があるとしても偶然の結果である)」
なぜ互いに相反する仮説を立てるのでしょうか。それは、対立仮説だけで仮説を検定することはできないからです。
「差がある」という対立仮説は「1円の差がある」、「2円の差がある」、・・・と無限の仮説の集まりです。無限の仮説をひとつひとつ検証することは不可能です。
逆に「差がない」という帰無仮説はただ一つの状態を表す仮説です。この「差がない」という仮説を検証し、否定されれば「差がある」という対立仮説を受け入れることができます。
帰無仮説が否定されるとき、帰無仮説を棄却するといいます。帰無仮説が否定できないとき、帰無仮説を受容するといいます。
仮説検定の手順2:基準を決める
そもそも「偶然による差」とはなんでしょうか。簡単な分析編で取り上げたように、データにはばらつきが生じます。以下のような状況を考えてみましょう。
まだ今月の売上データがない状態であると仮定し、さまざまな状況を考えて「今月の客単価が前年同月と同じ」と予測したとします。しかし、実際にデータを取ってみるとピタリと同じになることは滅多にないでしょう。いくらかは上下すると思います。
その上下幅が±1円くらいだと偶然そうなってもおかしくないと感じます。±10円くらいでも偶然と言えそうです。しかし±200円を超えるとそれはもう偶然ではなさそうですよね。つまり差が大きくなるにつれて、その差が偶然である確率が低くなります。
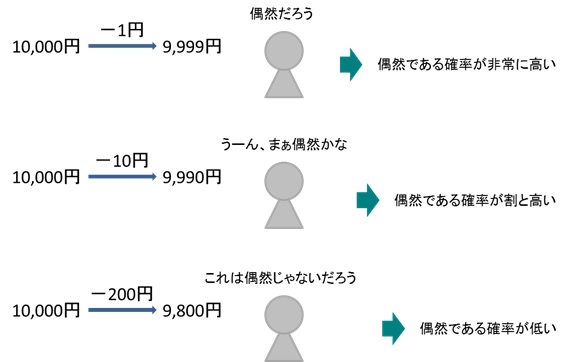
それでは、偶然である確率をどのように計算し、それが果たして高いのか低いのかどのように判断するのでしょうか。
もし仮に、同じ1ヶ月を何回も繰り返すチャンスがあり、その結果のうち100回は客単価に-200円の差が生じたとします。そしてその100回のうち3回は偶然-200円の差になったとしましょう。
この場合、「3%の確率で偶然-200円の差が生じた」と言えます。もちろん、この3回が偶然かどうかを直接判断することはできません。しかし、統計学的な計算を行うことで「差が偶然である確率」を算出することができます。この確率のことをp値と呼びます。
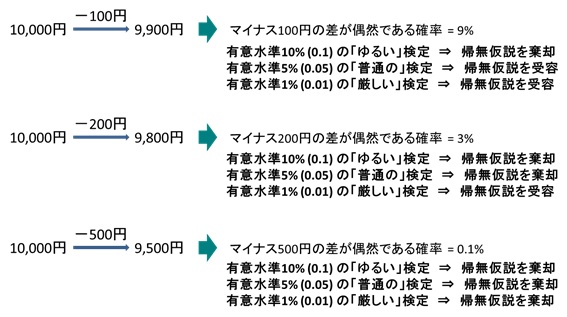
次に、「偶然である確率が3%」というのが高いのか低いのかを判断しなければなりません。そのためには、「偶然である確率が○%より小さいなら、それは偶然でないと判断しよう」というように、あらかじめ決めておく必要があります。この「○%より小さい」という基準のことを有意水準と呼びます。
p値が有意水準よりも小さい場合は、偶然とは認めず、差があると判断します(つまり帰無仮説を棄却します)。逆に有意水準よりも大きい場合は、偶然の差であると判断します(つまり帰無仮説を受容します)。この有意水準は勝手に決めてよいものですが、一般的には5%、厳しい検定には1%、ゆるい検定には10%が用いられます。
仮説検定の手順3:検定方法を決める
仮説検定では、現実に生じた差が偶然である確率、すなわちp値を次のように計算します。
- p値 =「現実に起こった現象が、帰無仮説のもとで起こる確率」
簡単な例を見てみましょう。

この例ではp値は0.0625(6.25%)と手計算で求めることができました。しかし、たいていの場合はp値の計算に統計学的な手法を用いなければなりません。この統計学的な手法のことを検定方法といいます。
そして、検定方法は、どのような帰無仮説を検定するのかによって非常に多くの方法から適切なものを選ばなければなりません。時には複数の検定方法の組み合わせによって検定する場合もあります。
このコラムでは、非常によく用いられるt検定とχ(カイ)二乗検定を紹介したいと思います。
t検定
t検定は一般的に2群の平均に差があるかどうかを検定するものです。「今月と前年同月の平均客単価の差」「今月と前年全体の平均客単価の差」「キャンペーン施策前後の顧客の購入意欲の変化」などを検定することができます。
ただし、データの分布が正規分布に従うという条件が必要となります。データの分布が正規分布に従わない場合、検定結果が誤っている可能性が高くなります。
χ二乗検定
χ二乗検定は、クロス集計の結果に対して全体の割合に差があるかどうかを検定するものです。たとえば、店舗Aと店舗Bの来客者の性別ごとの人数を集計した時に、次の結果になったとします。
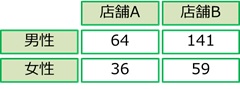
店舗AとBで男女の割合に差があるかどうかを検定するのがχ二乗検定になります。
ちなみにこのデータに対してχ二乗検定を行うと、p値は0.31(≒31%)と計算されます。有意水準を5%とすると、「男女の割合に差がない」という帰無仮説を棄却できません。ゆえに、「男女の割合に差があるかどうか判断できない」という結論になります。
「男女の割合に差があるかどうか判断できない」という回りくどい言い方をしたのは、本当は差があるかもしれないからです。今のデータでは、単にそれを証明するだけの十分な証拠がありません。また、どんなに工夫をこらしても、差がないという帰無仮説をデータから完全に証明することは不可能です。
χ二乗検定は2×2の集計に限らず、10店舗に対する来客者の年代ごとの人数といったクロス集計にも適用できます。
χ二乗検定は、全体として各グループ間に差があるかどうかを検定できますが、どのグループ間に差があるのかまでは分かりません。2×2の場合は2グループ(図の場合2店舗)しかないので、分かりやすいですが、3つ以上のグループになるとグループ間の差を検定する別の方法が必要になります。
ただし、グループ間の差を検定する場合にも、まずはχ二乗検定で全体の中で差があることが言えないと検定をする意味がありません。
t検定とχ二乗検定の紹介をしました。
後半のコラムでは、実際のデータを用いてt検定とχ二乗検定を行いたいと思います。
アサインナビでは、データサイエンスに関するセミナーを随時開催しております。
過去には、データサイエンティストの知識を習得するための実践塾や、特別講師を招いてのセミナーなどを開催しております。
過去の様子はこちらからご確認いただけます。
▼データサイエンティスト実践塾▼
第1回データサイエンティスト実践塾を修了しました!
▼データサイエンスの現状と未来▼
シリコンバレーに学ぶ、日本のデータサイエンスの現状と未来 ~これからのデータドリブンな時代に本当に必要なこと~を開催しました







