こんにちは。株式会社エル・ティー・エスの渡辺翔太です。
前回に引き続き、クラスター分析について解説していきます。クラスター分析は階層クラスター分析と非階層クラスター分析の2つに分けることができます。今回は実際に2つのクラスター分析をRで実行してみます。その際に気を付けるポイントとしてデータ間の距離についての話をしたいと思います。
■目次■
階層クラスター分析
階層クラスター分析とは、データ間やクラスター間の距離が最も小さいものから順次クラスターを形成する手法です。
クラスター内にクラスターが含まれる入れ子構造になっており、クラスターの最小単位は1つのデータとなります。階層クラスター分析によって得られるこの構造は次のような樹形図で表すことができます。
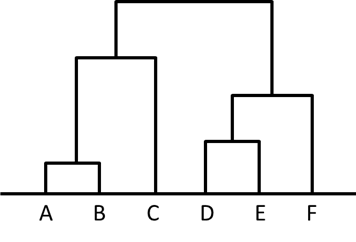
このような樹形図のことをデンドログラムといいます。また、この樹形図における各点のクラスターは次の散布図のように表現されます。
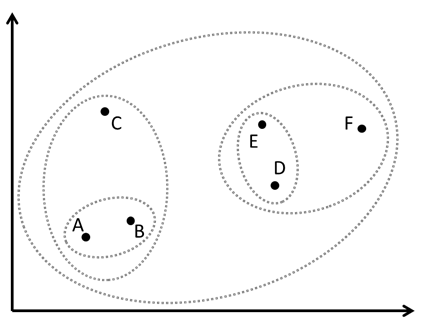
階層クラスターの作り方は、まず各データ同士の距離が最も小さいものをまとめます。この場合はAとBの距離が最も小さいので、AとBを一つのクラスターにまとめます。これを{AB}とします。
クラスターが生成されたら、それ以降はクラスターとデータ間、またはクラスター同士の距離を使用します。{AB}、C、D、F、Eの間で距離が最小となるのはEとDなので、クラスター{ED}を生成します。
次に距離が最小となるのは{ED}とFなので、クラスター{{ED}F}を生成します。このようにして順次クラスターを生成することで、最終的にひとかたまりのクラスター{{{AB}C}{{ED}F}}ができました。
デンドログラムにおいてその高さはクラスター間の距離を表します。そのため、適当なところで横線を引くことによってクラスターの数を決めることができます。
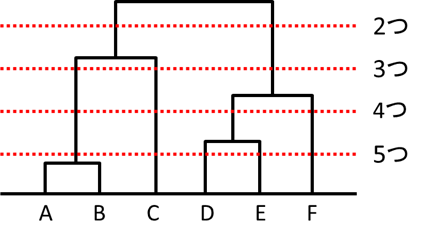
今回のケースでは2~3のクラスターに分けるのがよさそうですが、実際には各クラスター内のデータを見てクラスターの特徴から判断する必要があります。
さて、階層クラスター分析の計算に必要な、データ間の距離およびクラスター間の距離について説明していきます。基本的に階層クラスター分析は、
- ①任意の2つのクラスター内にある全データ間の距離を計算する ※クラスターになっていないデータはそのデータしか含まれないクラスターとみなす。
- ②”もっとも近い”2つのクラスターをまとめて一つのクラスターとする
この2つの計算の繰り返しです。
まず①で「任意の2つのクラスター内にある全データ間の距離を計算する」ためには、データ間の距離を決める必要があります。列挙すると、
・ユークリッド距離
データの各要素間の差の二乗和をルートしたもの。ごく一般的な距離を表す。
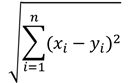
・最大距離
データの各要素間の差のうち、最大となるもの
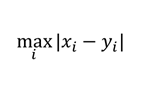
・マンハッタン距離
データの各要素間の差の絶対値の和
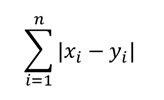
・ミンコフスキー距離
次の式で定義される距離で、ユークリッド距離・最大距離・マンハッタン距離の一般化(それぞれp=1、p=2、p=∞)
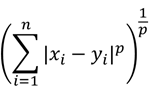
・マハラノビス距離
次の式で定義される距離
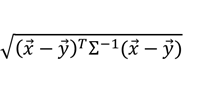
※Σは共分散行列
・コサイン類似度
次の式で定義される値。-1~1の間を取る値で、値が大きいほどデータが似ているため類似度という。
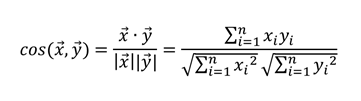
このようにいろいろな距離の定義があります。どの距離を用いるのが最適かは分析の結果次第で変わるため、さまざまな距離で分析しビジネスに適した距離を選択する必要があります。
次に②の「”もっとも近い”2つのクラスターをまとめて一つのクラスターとする」について、”もっとも近い”の考え方にもいろいろあります。Rで実行できる方法を列挙します。
・最近隣法
任意の2つのクラスター内のデータ同士で、最も近いデータ間の距離をクラスター間の距離とみなす。そのときに、クラスター間の距離が最小となる2つのクラスターを一つにまとめる。
※クラスター間の距離が最小となる2つのクラスターを一つにまとめるのはこれ以降の方法でも同様
・最遠隣法
最近隣法とは逆に、任意の2つのクラスター内のデータ同士で、最も遠いデータ間の距離をクラスター間の距離とみなす。
・群平均法
任意の2つのクラスター内のデータ同士の距離の平均値をクラスター間の距離と見なす。
・重心法
クラスター内のデータの重心(各データ項目について平均した点)を求め、任意の2つのクラスター内の重心同士の距離をクラスター間の距離と見なす。ただし、クラスター内のデータ個数で重みを付けるようにする。
・メディアン法
重心法で距離を計算する際の重みをクラスター間で等しくした場合の方法。
・ウォード法
2つのクラスターをまとめたときに、データのばらつきが小さいクラスターになるようにまとめる方法。この方法は多くのケースで分類の精度が良いといわれている。
代表的なものは以上となりますが、ほかにもいろいろな手法が開発されています。
データ間の距離の定義、および2つのクラスターのまとめ方についてそれぞれ検討する必要があり、また、組合せによって結果は変わってしまいます。どの手法を選択すればよいのかは、勘と経験に頼ることが多いです。
階層クラスター分析の実行
さて、階層クラスター分析をRで実行してみましょう。
今回はRにデフォルトで入っており、よくデモデータとして使用されるirisデータで実行してみたいと思います。
まずはデータを確認しましょう。データはirisという名前の変数に格納されたデータフレームになっています。setosa、versicolor、virginicaという三種類のアヤメにおける”がく”の長さと幅、および花弁の長さと幅が50個体ずつ計150個体のデータが格納されています。ここでは3個体ずつ表示させてみましょう。
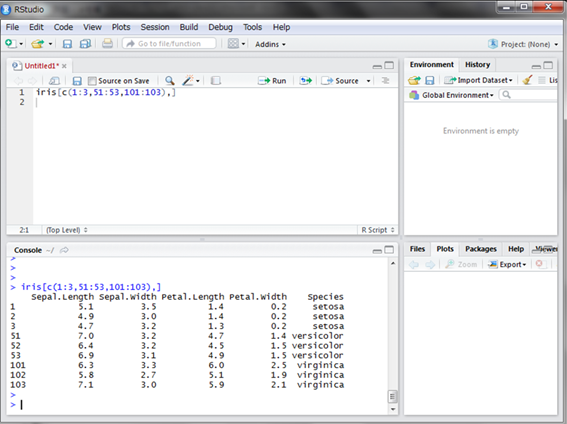
左4つの列が観測データ、最後の列が種類を表します。
さて、種類が分かっていないものとして、4つの観測データから似た個体を階層クラスター分析によってまとめることにしましょう。
さて、階層クラスターの手順は
- 任意の2つのクラスター内にある全データ間の距離を計算する
- ”もっとも近い”2つのクラスターをまとめて一つのクラスターとする
というものでした。ただ、クラスターを作る際にいちいちクラスター内のデータ間の距離を計算するのは手間が掛かるので、Rでは先に全データ間の距離を求めます。dist()関数を使用することで計算できます。
まず、観測データのみ抽出し、最初の5行分で距離を計算してみます。
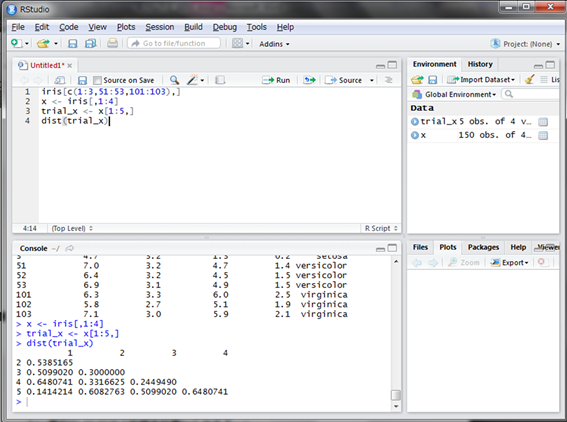
このように、各データ間の距離が行列のような形で計算されました。この形式のデータを150データ分で作成し、変数に格納します。なお、dist()関数の引数methodで距離の定義を選ぶことができます(デフォルトはユークリッド距離です。ここではマンハッタン距離にしてみましょう)。
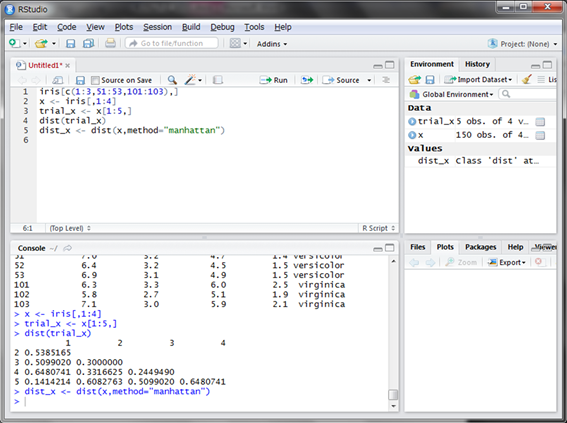
次に、階層クラスター分析を行ないます。使用する関数はhclust()関数です。引数methodでクラスター化の方法を選択できます(デフォルトはcompleteとなっており、最遠隣法を指します。)。
ここではデフォルトのままで実行したいと思います。
変数hclust_xに格納し表示しましたが、このままでは特に情報は見られません。しかしこの変数をplot()関数に入れて実行する(plot(hclust)と入力し実行する)とデンドログラムを描画することができます。
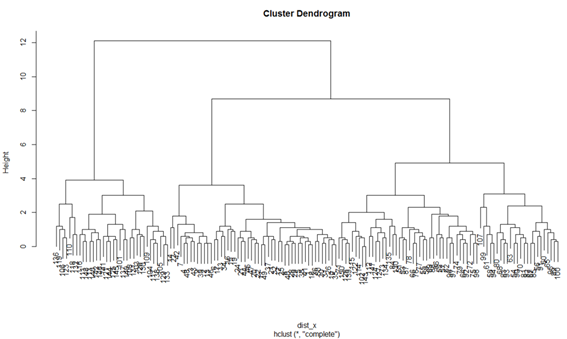
これで階層クラスター分析がまずは完成しました。あとは、クラスターの数を適当に決め、その中に含まれるデータの情報を読み解くことでどのような特徴を持ったクラスターに分かれているかを判断していきます。
なお、cutree()関数という、クラスターの数に合わせてデータにラべリングしてくれる便利な関数があります。引数にhclust()関数の結果と分けたいクラスター数を指定します。
さて、irisのデータは実際には花の種類のデータがありました。この階層クラスタリングの結果が花の種類ごとになっているのか気になります。
描画したデンログラムにはデータ番号が表記されていますが、ここを花の種類にしてみます。そして、デンドログラムの起点が一致するように引数hangに-1を指定し、文字が被らないよう引数cexを0.7にします。
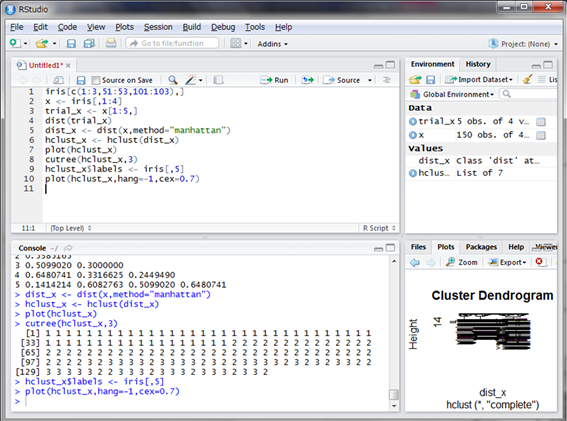
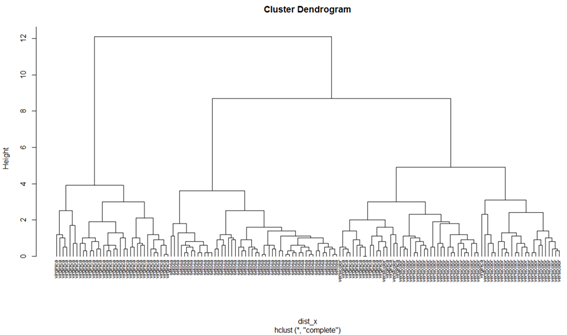
小さくて見えないですが、高さが6付近の部分で3つのクラスターに分けてよく見てみると、左がvirginicaのクラスター、中央がsetosaのクラスター、右がversicolorにvirginicaが一部混ざったクラスターになっています。
このことから、setosaは他の2種と比べて特徴が大きく異なっていることや、virginicaの中にはversicolorと特徴が似ている個体と似ていない個体が存在していることが見て取れます。
他の距離やクラスター化方法を組み合わせても、だいたい似たような結果になることが分かりますので、ぜひ挑戦してみてください。これで階層クラスター分析は終わりです。
非階層クラスター分析
データが150程度であれば計算もストレスなく実行されますが、これが何千、何万にもなるとデータ間の距離を求めるのに非常に時間が掛かってしまいます。そのため、ビッグデータの時代に階層クラスター分析は適さない可能性があります。
大量のデータでも、より高速にクラスタリングする方法が非階層クラスター分析です。非階層クラスター分析の代表例であるk平均法を紹介します。k平均法はk-means法とも呼ばれ、あらかじめクラスターの数を指定するとそのクラスター数になるようにクラスタリングされます。
以下にアルゴリズムを記載します。
- ①決められたクラスター数をkとする。最初にk個点を選ぶ。これをクラスターの中心の初期値と定める。
※このとき、データからk個ランダムに選ぶ場合や、データに限らず適当な数値を持つ点を選ぶ場合などがあります。 - ②各データに対しk個の中心との距離を計算し、最も近い中心のクラスターに各データを振り分ける。
- ③k個のクラスターができるので、各クラスターの中心を求め、クラスターの中心を更新する。この時、各データの平均を中心として用いる。
- ④②と③を、中心点が変化しなくなるまで、つまりクラスター内のデータが移動しなくなるまで繰り返す。
以上が理論です。ここでもデータと中心との距離をどの定義にするかや、中心の決め方をどうするのかなど決めることが多いですが、まずはRのデフォルトでk平均法を実行してみましょう。
分かりやすいように、今回もirisの観測データを使います。使うのはkmeans()関数で、データとクラスターの数を引数で指定します。
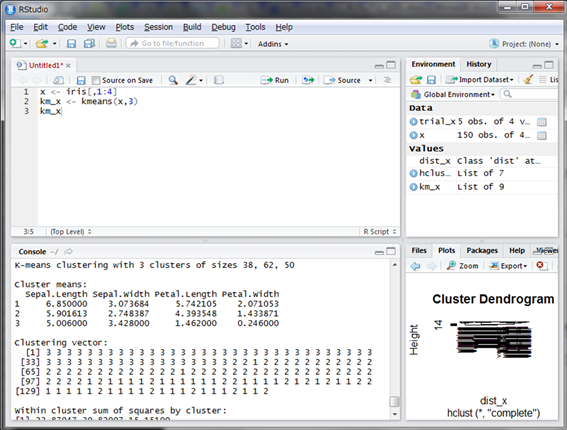
結果を見てみると、Clustering vectorという部分にクラスター番号が付与されています。花の種類とクラスタリングが一致しているか見てみましょう。Cluster番号と花の種別でtable()関数を使用します。
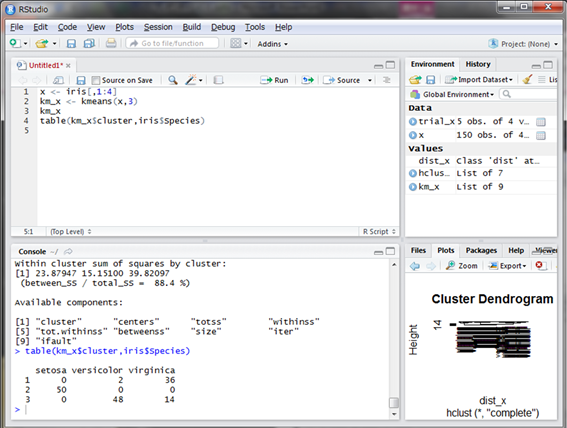
setosaは完全にクラスターとして分かれていますが、versicolorとvirginicaはうまく分離できていません。これは階層クラスター分析の結果ともよく一致しています。
ところで、うまく分離できなかったのは手法の問題でしょうか。それももちろんあるのですが、やはりデータそのものが似ていないのかもしれません。
しかし、データが似ていないことは悲観すべきことではありません。virginicaの個体の中にはversicolorに近い遺伝子を持っているものと遠い遺伝子構造になっているものがいるのではないか、それは生育環境や地域が関係しているかもしれない、といった今後の活動への示唆を与えてくれるのです。
では、クラスター分析はここまで。次回は確率分布編です。これまでとは少し違って、そもそもデータって何なのか、そして確率がどうかかわってくるのかを学習します。お楽しみに。
アサインナビでは、データサイエンスに関するセミナーを随時開催しております。
過去には、データサイエンティストの知識を習得するための実践塾や、特別講師を招いてのセミナーなどを開催しております。
過去の様子はこちらからご確認いただけます。
▼データサイエンティスト実践塾▼
第1回データサイエンティスト実践塾を修了しました!
▼データサイエンスの現状と未来▼
シリコンバレーに学ぶ、日本のデータサイエンスの現状と未来 ~これからのデータドリブンな時代に本当に必要なこと~を開催しました







