こんにちは。株式会社エル・ティー・エスの渡辺翔太です。
今回は決定木学習と呼ばれる手法について説明していきたいと思います。
決定木学習は教師あり機械学習であり、目的変数の予測・分類に使用します。目的変数、説明変数ともにカテゴリ変数と量的変数(連続数値変数)の両方が許され、外れ値にも頑健なため昔からビジネスの世界において使用されてきた手法です。
決定木学習の概要
「決定木」という名前の由来は、英語のDecision Treeをそのまま日本語訳したものになります。本来Decision Treeは、意思決定の際に起こりうる事象に対して、あらかじめ行動を計画するものでした。例えば明日の予定を決める際に、「明日の天気が晴れか曇りだったら海に行き、雨だったらどこへも行かない」という計画を作っておき、明日の天気次第で行動を選択します。さらに「晴れの時は気温が25℃より高いときのみ海に行き、曇りの時は気温が30℃より高いときのみ海に行く」のような詳細な計画も立てるでしょう。これを図示すると次のような樹木モデルとなります。
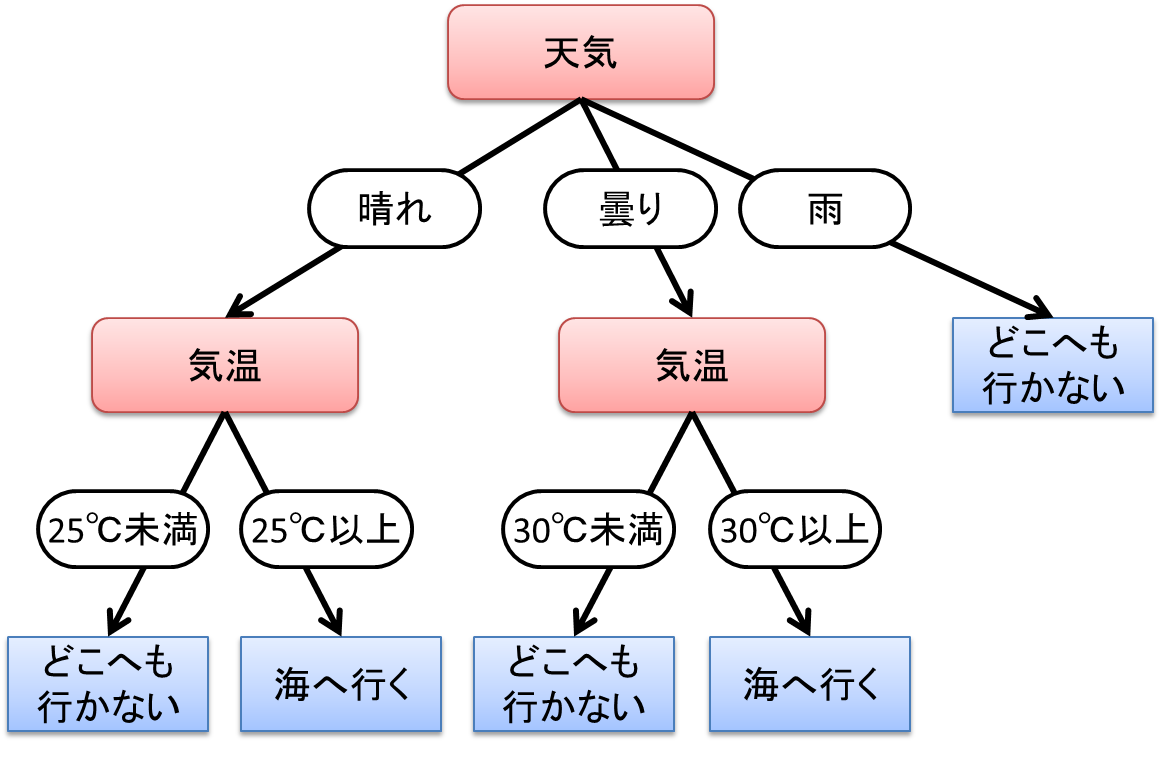
本来は人が条件から行動を計画しそれを可視化するモデルでしたが、これを機械学習に応用したのが決定木学習です。決定木学習ではデータから次の”?”の部分を決めます。
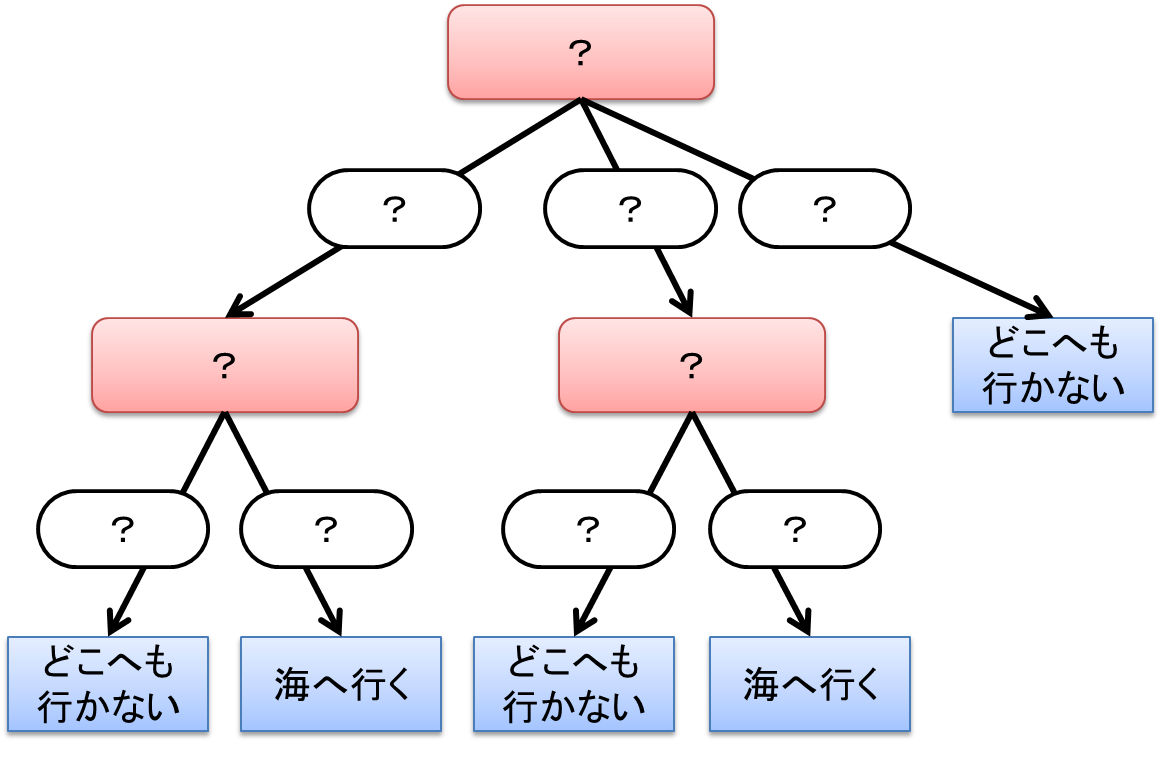
つまり、どの変数がどういった値(条件)のときに、行動(結果)が変わるのかを学習によって決めます。
分岐の決め方は、各分岐によってデータを分割した時に、より結果が偏る(一つのカテゴリまたは値に決まる)ようにアルゴリズムが作られています。
詳細なアルゴリズムについては割愛し、まずは感覚を掴むために実践してみましょう。
Rで決定木学習を実践する方法
これまで説明してきた手法は、Rをインストールするとデフォルトで使用できる関数のみで実行することができました。しかし決定木学習はRのデフォルトでは関数が用意されていません。では、いちから自分でアルゴリズムを作らなければならないのでしょうか。それは大変ですよね。実はRにはパッケージというものが用意されており、用途に応じた関数やデータセット、オブジェクトなどが格納されています。このパッケージをインターネットを介してダウンロードしPCにインストールすることで、パッケージに格納されているデータや関数をこれまでと同じように利用することができます。ややこしく感じるかもしれませんが、実際にはとても簡単にできます。
決定木学習用のパッケージをインストールしてみましょう。パッケージ名は{rpart}といいます。インターネットに接続した状態でinstall.packages()関数を使用するだけです。引数にインストールしたいパッケージ名を文字列で与えます。
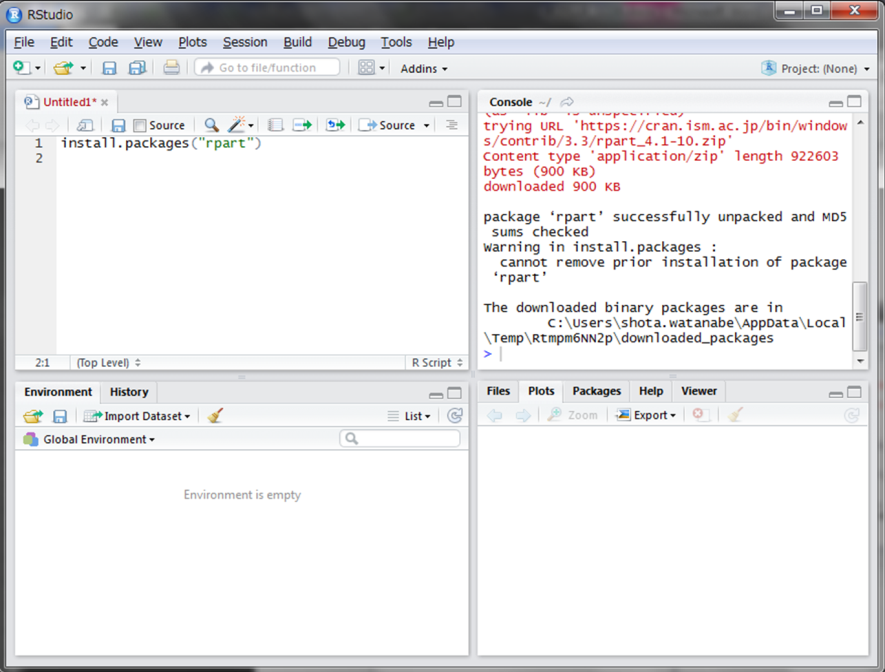
Console上にずらずらと記載されますが、”successfully unpacked”という言葉がどこかに出てきていたらひとまず成功です。この操作は、インストールが成功していれば一度で終わりです。次回からは同じパッケージをインストールする必要はありません。インストールされたパッケージを使用するには、R上に呼び出す必要があります。それはlibrary()関数にパッケージ名を文字列ではなく変数名として引数に与えます。
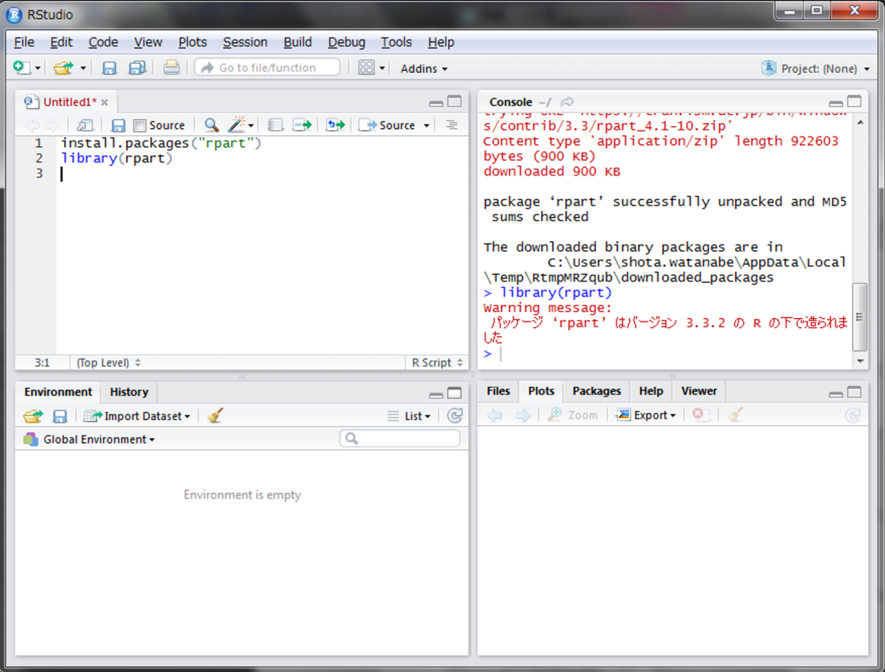
何も表示されないか図のようなWarning messageが表示された場合は呼び出し成功です。一方、Error messageが表示された場合はインストールがうまくできていないのでやり直してください。なお、library()関数での呼び出しにはインターネット接続している必要はありません。ただし、Rを起動するごとにlibrary()関数による呼び出しが必要となります。
ついでに、決定木をグラフで表すための{partykit}というパッケージもインストールし、呼び出しておきましょう。
さて、まずはおなじみのirisデータで実践してみたいと思います。irisはあやめの花の種類と、がく片および花びらの長さと幅の計測データが格納されているデータフレームです。
それぞれの計測データから花の種類を分類する決定木を作成したいと思います。使用する関数はrpart()関数です。回帰分析のときと同様に、目的変数~説明変数という形の引数を指定します。目的変数以外の変数すべてを説明変数にするには、ピリオドを使います。
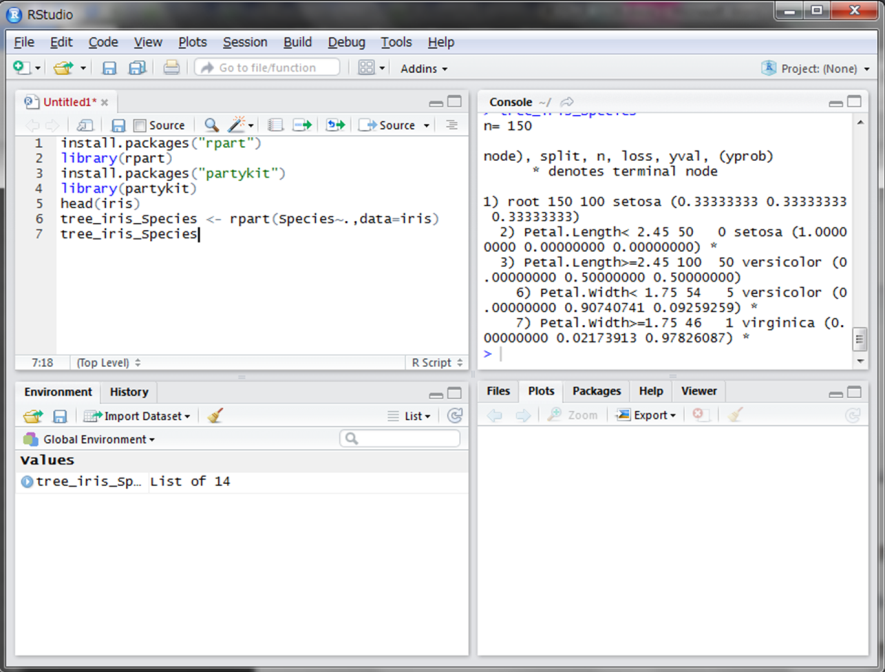
tree_iris_Speciesに結果を格納し表示させました。これを見てもよく分からないので、実際に決定木を作成します。as.party()関数の引数に先ほどの変数を代入したものをplot()関数の引数として与えます。
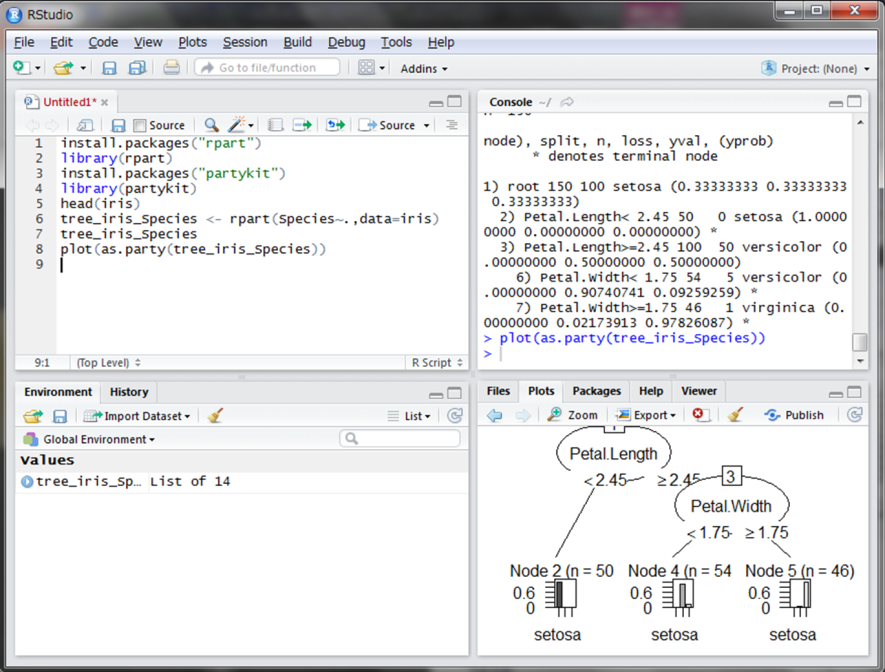
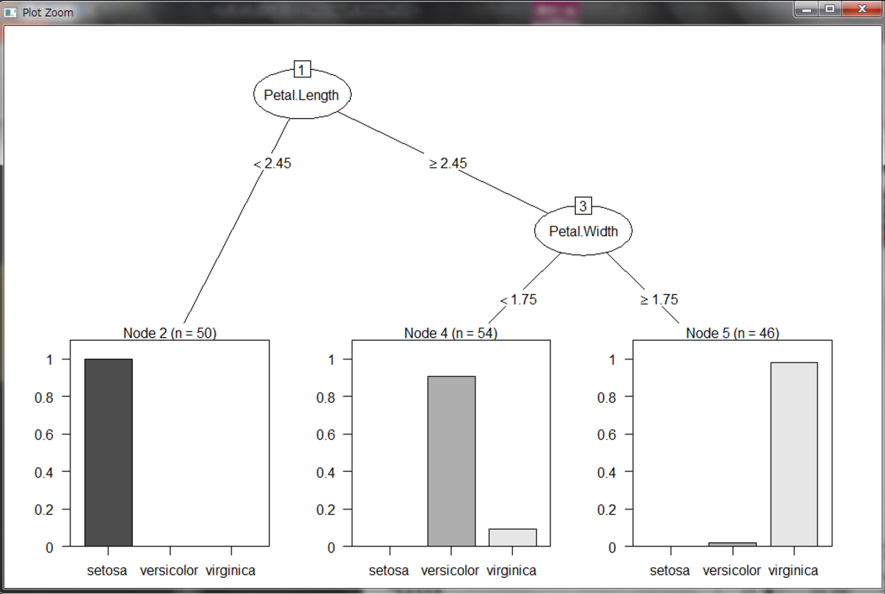
このような決定木が作成できました。これを見ると、Petal.Lengthが2.45未満の場合はすべてsetosaという種類であり、Petal.Lengthが2.45以上の場合はさらにPetal.Widthが1.75未満で約90%がversicolor、1.75以上でほとんどがvirginicaと分類されました。つまり、あやめの種類を分類するには、まずPetal.Lengthの大きさでsetosaかどうかを判断し、Petal.Widthの大きさでversicolorかvirginicaかを判断するのが最適なルールということが分かります。
さて、目的変数をカテゴリ変数にしましたが、目的変数が連続的な数値だった場合はどうなるでしょうか。今度はPetal.Lengthを目的変数にしてみます。
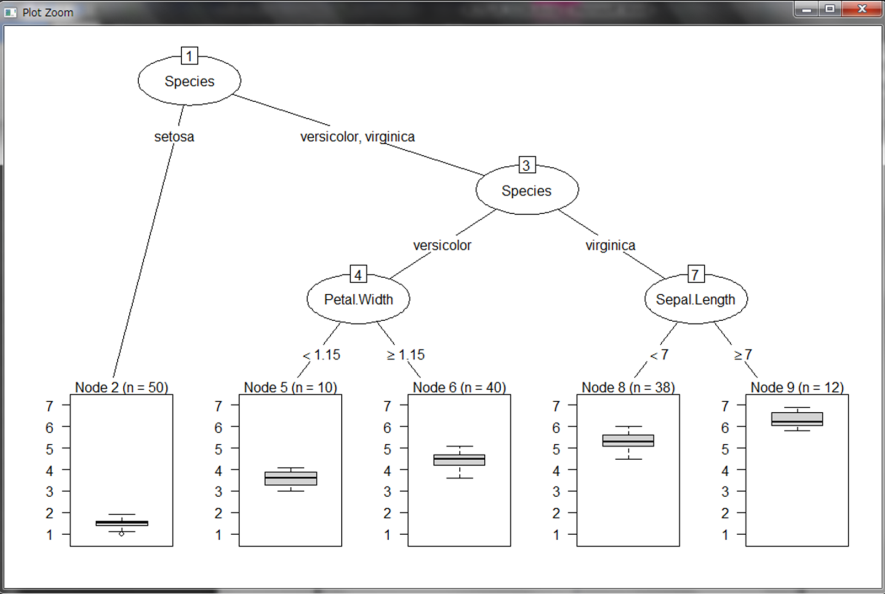
今度はこのような決定木となりました。
これは箱ひげ図と呼ばれるグラフで、データの特徴を表しています。詳しくは各自調べていただくとして、中央の太い黒線がそれぞれ分岐したデータにおけるのPetal.Length平均値を表しています。たとえば種類がversicolorの中でもPetal.Widthの大きさによってPetal.Lengthの大きさに違いがありそうということが分かります。
さて、いつもirisのデータを使用していても面白みがないので、他のデータでも実践してみましょう。Rに標準搭載されているesophというデータを使います。これは、肺がんの羅患状況を示しています。
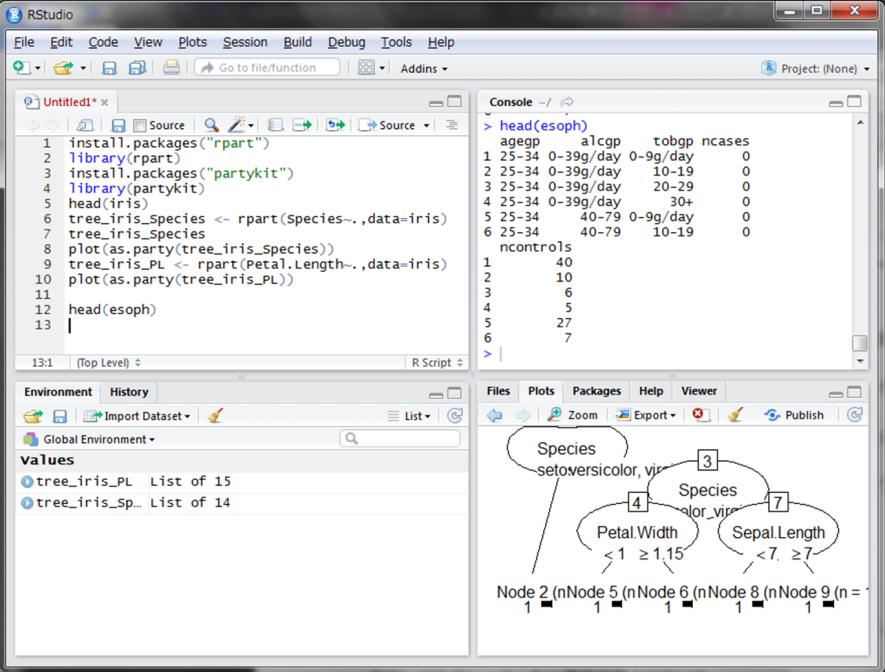
agegpが年齢層、alcgpが1日あたりのアルコール摂取量、tobgpが1日あたりの喫煙量を示しています。そしてncasesが発症数、ncontrolsが検査個体数を示しています。つまり、1行目の25-34歳、アルコール摂取量0-39g/day、喫煙量0-9g/dayのグループは40人検査し、発症数0人だったというデータになります。このデータは集計されているため、そのままでは決定木学習に使用できません。検査個体ごとのデータになるように次の前処理を行ないます。各前処理の詳細は割愛しますが、最終的に得られたデータセットesoph.dtを見ていただければ分かると思います。

肺がんの羅患状況はcaseという列名にしています。このcaseを決定木で分類してみましょう。
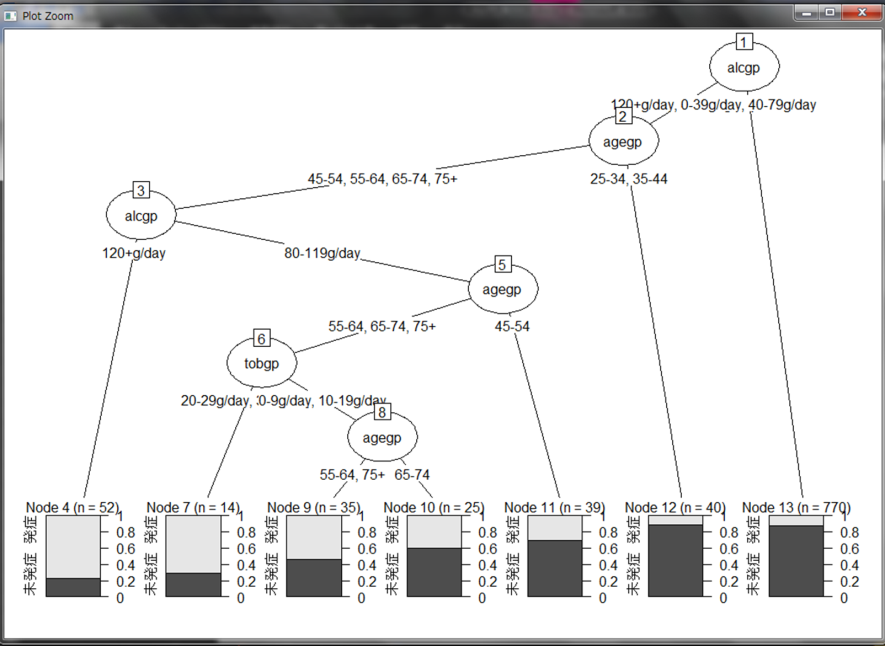
やや分岐の多い複雑な決定木となりました。結果は未発症が黒、発症がグレーの割合で表現されています。そして驚くべきことは、肺がんの羅患状況にもかかわらず喫煙量に関する分岐がひとつもありません。アルコール摂取量と年齢層に依存していることが分かります。
決定木がやや複雑で、文字も重なって見えづらいので、もう少しシンプルにしてみたいと思います。文字通り、木の剪定を行います。まずplotcp()関数に結果を代入します。すると下図のようなグラフが作成されます。
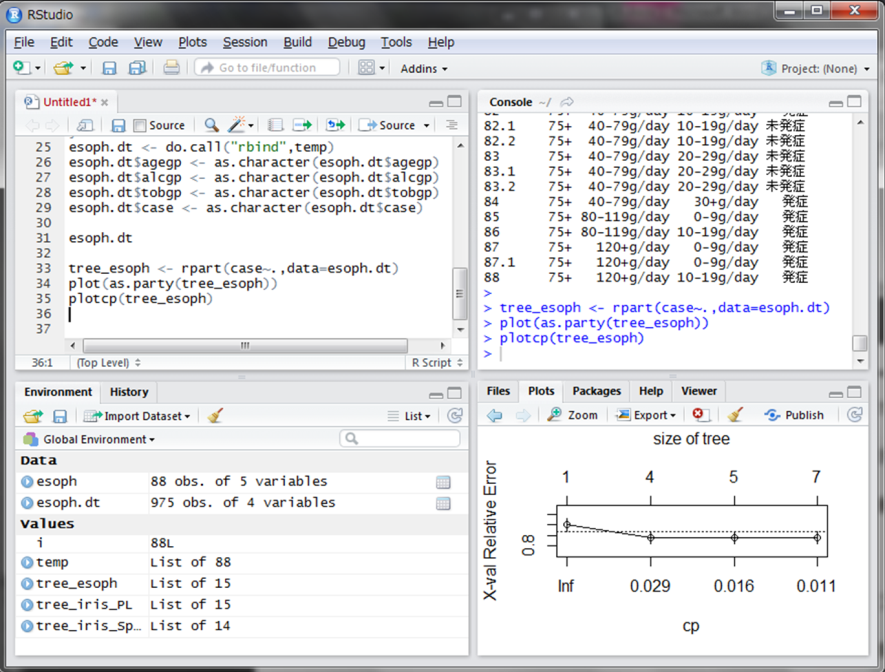
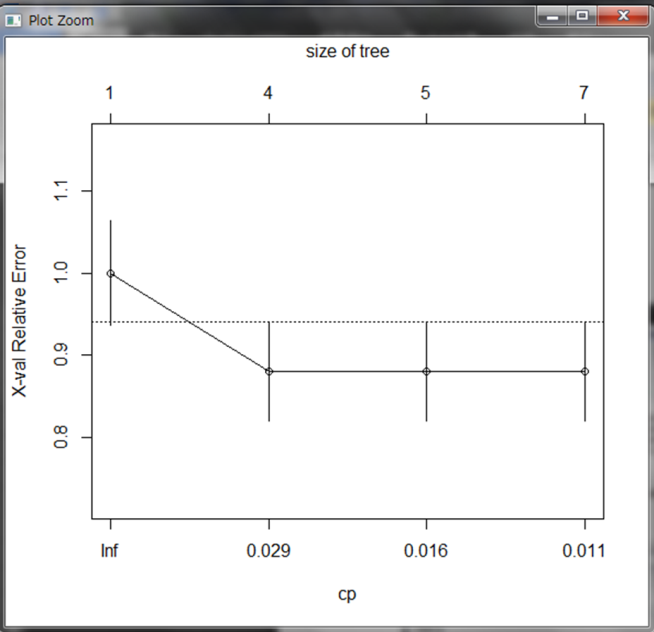
このグラフは木の大きくしていったときの相対的な誤り率を示しています。
木の大きさを4以上、つまり分岐先を4つ以上作成しても誤り率は低下しないことが分かります。また、点線は木の大きさを決める目安となる線で、この線を下回った直後の大きさが、最もシンプルに表現できているといえるようです。ここで、木の大きさが4のときがよさそうなので剪定します。木の剪定にはprune()関数を使用します。第一引数に決定木の変数、cpという引数には先ほどのグラフにおける木の大きさが4のときの下横軸の値を指定します。ここでは、グラフからcp=0.029と読み取れます。その結果をtree2_esophとい右辺数に代入し、同じようにグラフ化してみます。
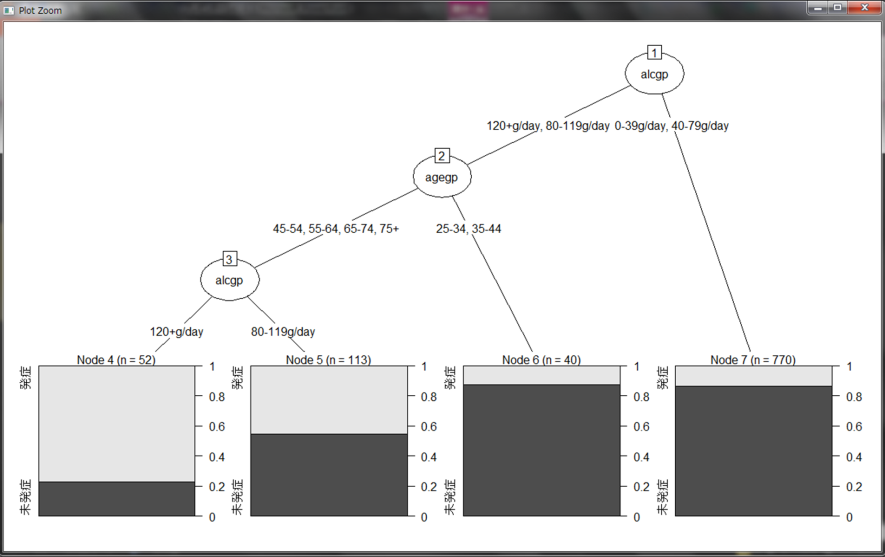
よりシンプルに表現されています。この結果を解釈すると、「アルコール摂取量が1日80g未満ならば約15%の発症率であり、アルコール摂取量が1日80g以上でも年齢が45歳未満であれば同じく約15%の発症率である。45歳以上になると1日120g未満のアルコール摂取量であれば発症率45%だが、120g以上だと発症率80%となる」というように分析できます。この研究結果だけから結論付けると、肺がんにならないためにはアルコール摂取量を控えることが重要であることがいえます。
決定木学習は結果の解釈性が高いため、原因分析などによく用いられます。一方でデータの品質によって結果が安定しなかったり、精度が悪かったりするので、その場合は他の手法を用いることになります。目的変数、説明変数ともにカテゴリ変数と量的変数のどちらも使用でき、外れ値にも強いため、分析の取っ掛かりに用いてみてはいかがでしょうか。決定木分析はここまでです!次回もよろしくお願いします!
アサインナビでは、データサイエンスに関するセミナーを随時開催しております。
過去には、データサイエンティストの知識を習得するための実践塾や、特別講師を招いてのセミナーなどを開催しております。
過去の様子はこちらからご確認いただけます。
▼データサイエンティスト実践塾▼
第1回データサイエンティスト実践塾を修了しました!
▼データサイエンスの現状と未来▼
シリコンバレーに学ぶ、日本のデータサイエンスの現状と未来 ~これからのデータドリブンな時代に本当に必要なこと~を開催しました







