こんにちは。株式会社エル・ティー・エスの渡辺翔太です。
前回は仮説検定についてコラムを書きました。今回は回帰分析について学んでいきたいと思います。
回帰分析とは
回帰分析とは、2種類以上のデータの比例的な関係(一方が増えるともう一方も増えるor減るといった関係)を分析する方法です。
たとえば、気温が高くなるとアイスクリームの売上が増加すると言われれば、ほとんどの方はうなずくでしょう。けれども、気温が1度高くなるとアイスクリームの売り上げがいくら増加するかと問われても、パッとは答えられないと思います。
その疑問に答えてくれるのが回帰分析であり、気温が1度上がるごとにアイスクリームの売り上げがいくら増加するのかが明らかになります。さらに、気温が○℃のときの売上を予測する式(モデル)を作ることもできます。
他の例を考えてみましょう。あなたは、ある地域における賃貸住宅の家賃相場を調べることになりました。家賃の値段はさまざまな要因によって変動します。駅からの距離、床面積、バストイレ別、など、いろいろな要因が考えられますね。
もちろん、すべての要因が家賃に影響を与えているとは限らないでしょう。対象の地域において、どの要因が家賃の値段に影響を与えているか、その影響度とはどの程度のものなのかを知ることができれば、希望の条件を満たす物件の家賃相場が計算できます。
気温とアイスクリームの売上の話では、気温を基準に売上を考えます。このように、売上というデータに対し気温という1つの要因の影響を分析する方法を単回帰分析といいます。
一方、家賃相場の話では、駅からの距離や床面積など複数の要因をもとに家賃を考えます。複数の要因が与える影響を分析する方法を重回帰分析/といいます。
また、売上や家賃のように他の要因から影響される変数を目的変数、目的変数に影響を与える変数を説明変数といいます。
今回はサンプルデータをもとに、アイスクリームの売上と気温の関係を単回帰分析で、家賃と複数の要因の関係を重回帰分析で明らかにしていきたいと思います。
アイスクリームの売上(単回帰分析)
次のCSVファイルには、2014年の日ごとの最高気温とその日のある店舗におけるアイスクリームの売上が記録されています。
CSVファイルはこちらからダウンロードいただけます。右クリックからデスクトップに保存してください。
早速データを読み込みの中身を見てみましょう。まずは上記ファイルをダウンロードしデスクトップに移動してください。次にRStudioを立ち上げ、スクリプト画面に図のようにコマンドを打ち込みます。
このとき、setwd()関数の中に使用PCのデスクトップを示すパスを記入してください。実行は、コマンドが記入された行を選択し「Ctrl+Enter」です。実行結果は下のコンソール画面に表示されます。
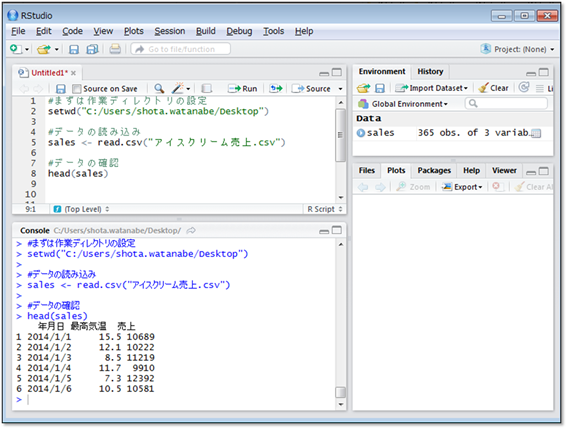
head()関数で6日分のデータを表示していますが、実際には日付、最高気温、売上が365日分入力されています。
早速、最高気温と売上の関係を単回帰分析してみましょう。回帰分析を行うlm()関数がRには用意されています。使い方は、
- lm(目的変数の列名~説明変数の列名,data=データの変数名)
と打ち込み実行するだけです。
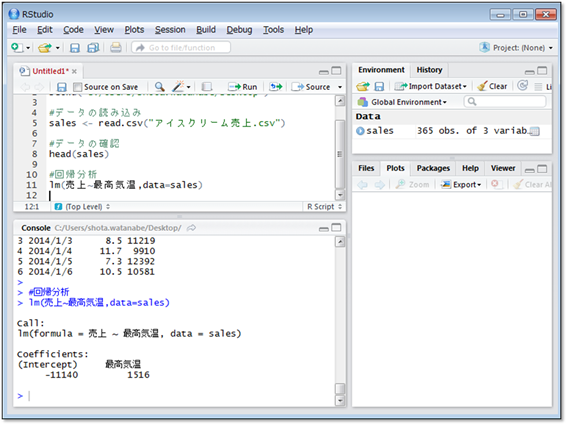
この結果の解釈は次のように考えます。
- (アイスクリームの売上)=(最高気温)×1,516円 - 11,140円
つまり、最高気温が1℃上がると売上が1,516円増えることになります。この結果をさらに詳しく見るために、lm()関数の結果の詳細を表示するsummary()関数を使ってみましょう。
一度lm()関数の結果を変数(ここではres1)に格納し、summary()関数の引数に指定します。
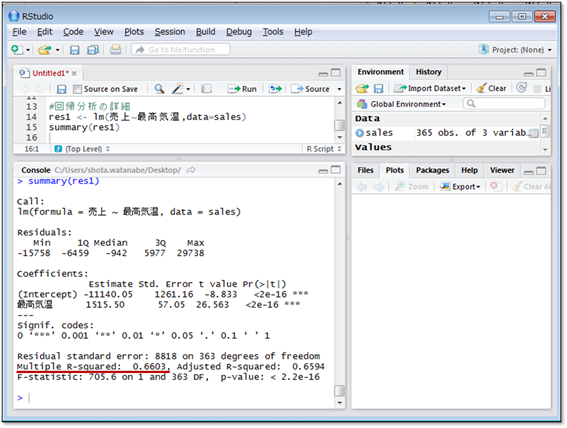
下線のMultiple R-squaredというのは、回帰分析で重要な数値であり、決定係数(または寄与率やR²値)といいます。
この数値は説明変数が目的変数をどの程度説明できているかを表しており、0から1の間の値をとります。決定係数が0に近いほど説明変数は目的変数にほとんど影響しておらず、1に近いほど目的変数は説明変数でほとんど説明できていることになります。
今回の結果では0.6603となり、まずまずの結果となりました。決定係数と回帰分析の良し悪しの目安は次の表のようになります。
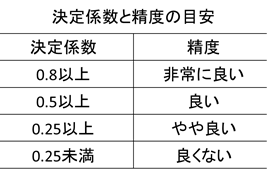
しかし、今回の結果だと最高気温が0℃のときの売上予測がマイナスとなってしまいます。一体どうなっているのでしょうか。
これは、実際のデータがどのようなものかを理解せず闇雲に回帰分析を行なったことに起因します。そもそも、回帰分析は、説明変数が1単位増加すると、目的変数がどの程度変化するかという比例関係を分析する方法です。そのため、データが直線的でないと分析することができません。
今回のデータが直線関係にあるかどうかを確認してみましょう。最も簡単な方法はグラフを作成することです。
売上を縦軸、最高気温を横軸にしたグラフを作成するには、plot()関数を使います。
- plot(縦軸にしたい列名~横軸にしたい列名,data=データの変数名)
という使い方をします。
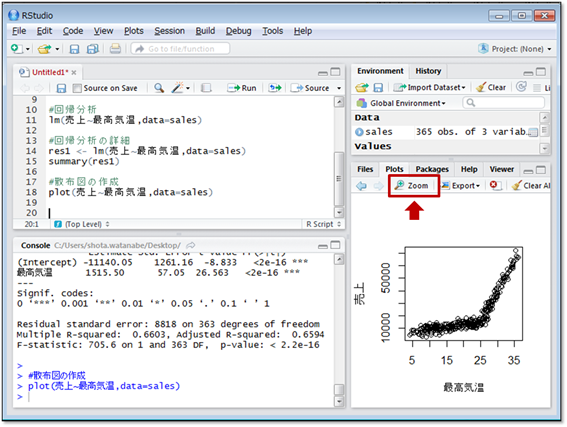
Zoomボタンを押すとグラフが拡大します。
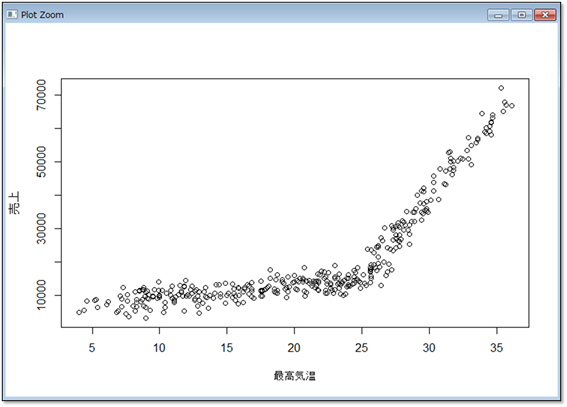
グラフを見ると、最高気温が25℃までは緩やかに売上が増加し25℃を超えると気温とともに急増することが分かります。つまりデータ全体では直線関係にあるとは言えませんが、「最高気温25℃」を基準に分割することで直線関係のあるデータになることが分かります。
最高気温が25℃以上のデータだけ取り出して回帰分析を行なってみましょう。
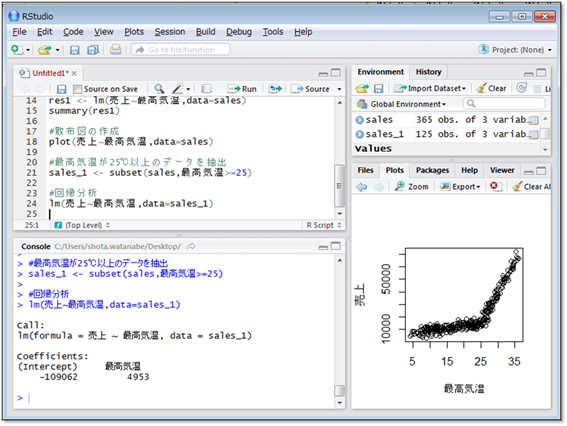
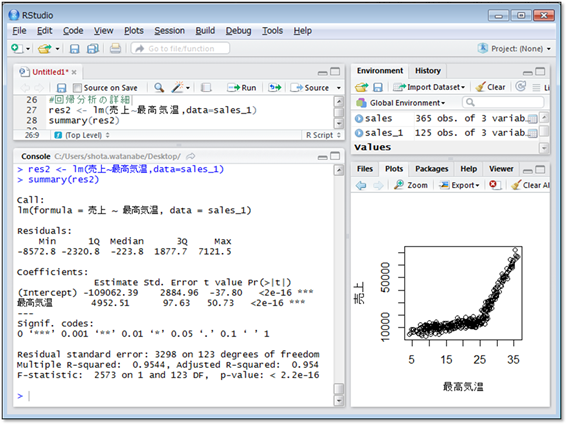
回帰分析の結果から、最高気温が25℃以上のときは
- (アイスクリームの売上)=(最高気温)×4,953円-109,062円
と表され、決定係数は0.9544と非常に良い結果となりました。この式を用いると、最高気温が1℃上昇すると売上が4,953円増えることが分かります。また、明日の最高気温が32℃と予想される場合は、
- (アイスクリームの売上)=32℃×4,953円-109,062円=49,434円
と売上の予測もすることができ、適切な発注管理や在庫管理につながります。
家賃相場(重回帰分析)
続いて、家賃相場に影響を与える要因と、その影響度を重回帰分析で明らかにしたいと思います。
次のデータは、100の物件の家賃・床面積・築年数・徒歩分数・エアコン有無・バストイレ別のデータが入力されています。
※データが入力されたCSVファイルはこちらからダウンロードいただけます。右クリックからデスクトップに保存してください。
床面積、築年数、徒歩分数は数値データなのでそのまま重回帰分析に使用できますが、エアコン有無とバストイレ別は「はい」か「いいえ」のどちらかを取るデータになります。このようなデータを説明変数に使用したいときは、「はい」を「1」に、「いいえ」を「0」に変換したダミー変数を用います。上記データはすでにダミー変数となっています。
早速データを見てみましょう。まずはファイルをダウンロードしデスクトップに移動してください。その後、データを読み込みhouserentという変数に代入します。
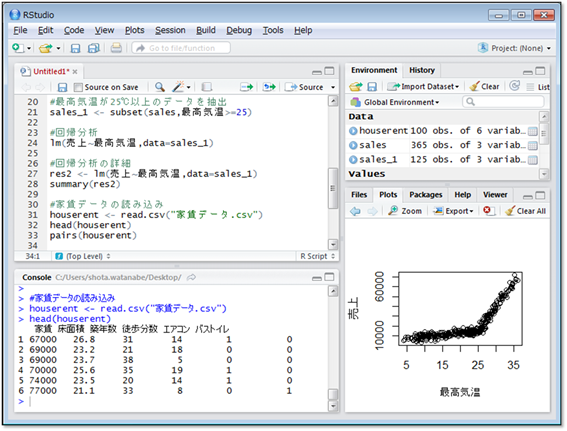
列名とデータがずれて表示されていますが、左から順に「家賃」「床面積」「築年数」「徒歩分数」「エアコン」「バストイレ」となっています。
ここで、重回帰分析で気をつけるべきことのひとつに、「説明変数同士で直線関係にあるものは、どちらかを除く」というものがあります。説明変数同士で直線関係にあるようなものが含まれると、重回帰分析の結果がおかしなことになってしまいます。この現象のことを多重共線性といいます。
多重共線性が起きないようにあらかじめ変数同士の関係を見ておきましょう。それには、pairs()関数を用います。pairs()関数の引数にデータを指定すると、各変数同士の散布図を作成してくれます。
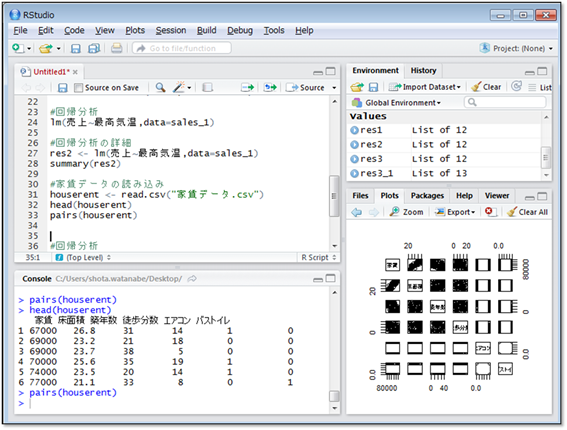
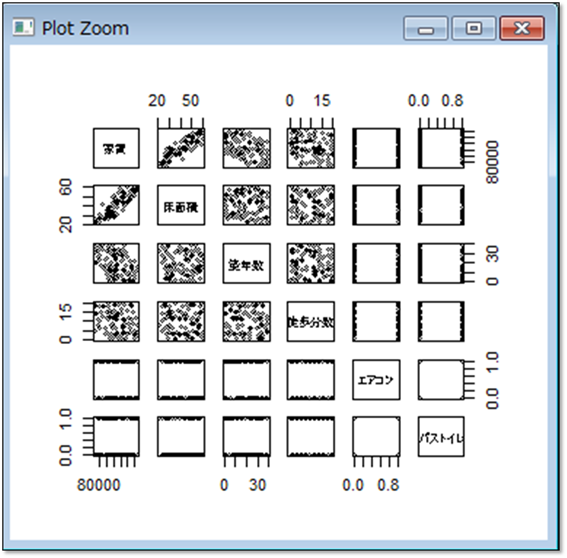
エアコンとバストイレはダミー変数となっているため傾向はつかみにくいですが、床面積・築年数・徒歩分数ではそれぞれの散布図を見る限り、直線関係は見られないようです。よって、全部の変数を説明変数に用いて重回帰分析を行なうことができます。重回帰分析を行なう関数もlm()関数です。使い方は、
- lm(目的変数の列名~説明変数1の列名+説明変数2の列名+…+説明変数3の列名,data=データの変数名)
というように、用いる説明変数の列名を+でつなげるだけです。また、すべてのデータを説明変数にする場合は、
- lm(目的変数の列名~.,data=データの変数名)
このようにピリオドで代用することができます。
今回は目的変数以外のすべての列を説明変数として使用し、重回帰分析を行なってみます。
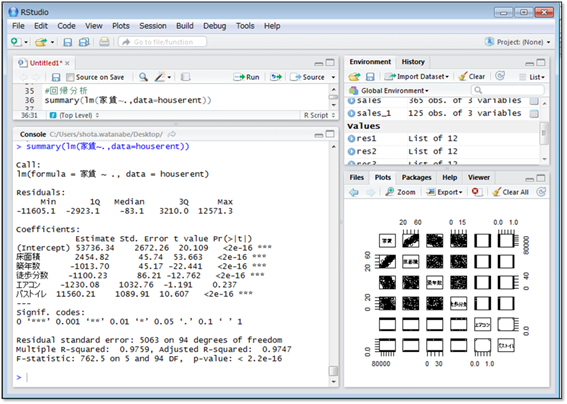
コンソール画面に結果が表示されます。Estimateという列がその説明変数の係数であり、1単位あたりの変化量を表します。
また、Pr(>|t|)という列は「係数が0である確率」を表し、p値と呼ばれます。係数が0とは、「説明変数が1単位変化しても、目的変数に何の影響も与えない」ということです。
エアコン以外のp値は「<2e-16」となっていますが、これは非常に0に近い値を表しています。エアコンのp値は約0.23と大きく、エアコンの有無は家賃に何の影響も与えない可能性が約23%と高いことを意味します。
このような目的変数に無関係な説明変数は取り除いて分析する必要があります。データから不要な説明変数を取り除き、改めて分析しても良いのですが、Rにはそれを自動で行なってくれるstep()関数というものがあります。
lm()関数の結果を変数(ここではres3)に代入し、その変数をstep()関数の引数に指定します。さらにstep関数の結果をres3_1に代入しsummary()関数で詳細化します。
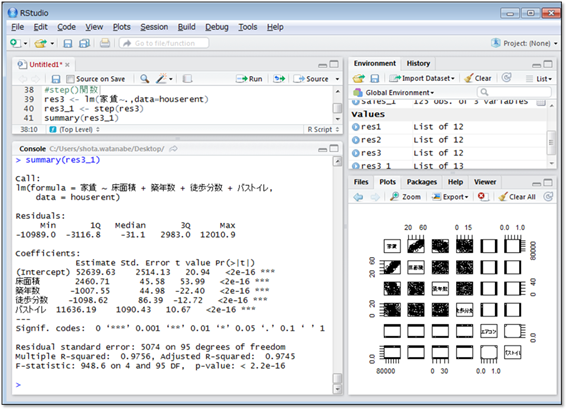
エアコンが説明変数から取り除かれた分析結果が得られました。
重回帰分析でも決定係数を見ることで、説明変数がどれほど目的変数を説明できているかを知ることができます。ただし、重回帰分析のときは、Multiple R-squared(決定係数)ではなくAjusted R-squared(自由度調整済み決定係数)を見ます。
これは、説明変数が多いほど決定係数の値が大きくなるという性質により、不要な説明変数を取り入れた分析結果のほうが決定係数が大きくてよい結果だという誤った解釈を生むからです。
そこで、説明変数の数も考慮して算出したのが「自由度調整済み決定係数」です。この数値を基に、説明変数がどれくらい目的変数を説明できているかを判断します。今回の結果では0.9745と非常によい結果となりました。
さて、分析結果からこの地域では、
- 「床面積が1m²広いと2,461円高くなる」
- 「築年数が1年長いと1,008円安くなる」
- 「駅からの徒歩分数が1分長いと1,099円安くなる」
- 「バストイレが別だと11,636円高くなる」
ことが分かります。
この結果をもとに家賃相場を計算する式は次のようになります。
- (家賃相場)=床面積×2,461円-築年数×1,008円-徒歩分数×1,099円+バストイレ(別なら1、ユニットなら0)×11,636円+52,640円
例えばお目当ての物件が「床面積30m²」「築年数5年」「駅から徒歩5分」「バストイレ別」であったとき、相場を計算すると127,566円となります。この物件の実際の家賃が100,000円だとすると相場より安いので借りたほうがよいという判断ができます。
いかがでしたでしょうか。今回はRを用いて回帰分析を行なう方法についてお伝えしました。
しかし今回行なった回帰分析は「線形回帰分析」というひとつの分析方法にすぎず、売り上げや家賃などの数値データのみが目的変数とすることができます。
「買ったor買っていない」や「見たor見ていない」などの2つに1つの状態を表すデータに対しては、「ロジスティック回帰分析」という方法を用いることで、どの要素がどの程度影響するのかを分析することができます。
次回はこの「ロジスティック回帰分析」について投稿したいと思います。長くなりましたが、次回もぜひご覧ください!
アサインナビでは、データサイエンスに関するセミナーを随時開催しております。
過去には、データサイエンティストの知識を習得するための実践塾や、特別講師を招いてのセミナーなどを開催しております。
過去の様子はこちらからご確認いただけます。
▼データサイエンティスト実践塾▼
第1回データサイエンティスト実践塾を修了しました!
▼データサイエンスの現状と未来▼
シリコンバレーに学ぶ、日本のデータサイエンスの現状と未来 ~これからのデータドリブンな時代に本当に必要なこと~を開催しました







