こんにちは。株式会社エル・ティー・エスの渡辺翔太です。
前回は回帰分析、特に「線形回帰分析」という分析手法について書きました。今回は「ロジスティック回帰」という手法について説明します。
また、このロジスティック回帰という手法は、最近では「機械学習」と呼ばれる手法のひとつとする記事も多くあります。そこで、機械学習とはいったい何なのかについても解説していきます。
機械学習とは
最近、機械学習という言葉がIT業界でもよく用いられるようになったと感じています。
名前だけ見ると、工場にあるような機械が学習するような印象がありますが、英語のMachine Learningの直訳表現に過ぎません。英語のMachineにはコンピュータやサーバなどの意味もあり、Machine Learningはコンピュータに学ばせる、コンピュータ学習などといった意味になります。
ではコンピュータに何を学ばせるのでしょうか。それは、データに潜む構造的なパターンや特性です。ただし、構造そのものを学習してくれるわけではありません。あくまで、ある構造を仮定したときに、その構造を決定する特性値を学習します。
例で示しましょう。前回の線形回帰分析も、見方によれば機械学習のひとつといえます。線形回帰分析の構造を仮定しなければなりません。
その構造とは、「(正規分布に従うと考えられる)数値データが、他の変数の一次結合(ある値を掛けて足し合わせること)によって表現される」というものです。では、この構造を決定する特性値とは、何でしょうか。それは、一次結合する際に変数に掛ける値となります。
前回のコラムでは、最高気温とアイスクリームの売上の関係について解説しました。売上は最高気温と直線関係にあることから、次のような式(つまり構造)を仮定したわけです。
- (アイスクリームの売上)=(特性値1)×(最高気温)円 + (特性値2)円
最高気温という変数に特性値1を掛けたものと、特性値2を足し合わせています。なお、特性値2は一般的に切片と呼ばれますが、これは“1“という変数に特性値2が掛けられたものと捉えてください。こうすることで、既存の変数では説明できない特徴を表現することができます。
構造を決めたら、あとはデータが構造に最も当てはまるような特性値1と特性値2を、データを用いてコンピュータが学習するというわけです。コンピュータが特性値を学習すると、データが持つ構造(数式)が決まります。
また、新しいデータが生成されたときにその構造に当てはめることで、結果を予測することができるというわけです。
この考え方が機械学習の本質となります。世の中のデータに潜む構造には様々なものがあります。
はじめに人間が構造を仮定する必要があることから、これまで多くの構造が考案されてきました。それらは一般的にはモデルと呼ばれています。線形回帰モデル、ロジスティック回帰モデル、ニューラルネットワークモデルなど、現在では多くのモデルが存在します。また、モデルを決定する特性値のことをパラメータと呼びます。
広義の機械学習は上記の理解で良いのですが、狭義には線形回帰モデルは機械学習に含まれません。実は線形回帰モデルはパラメータがデータの関数として一意に決まります(データを決まった数式に入れるだけでパラメータが求まってしまいます)。
一方、ロジスティック回帰の場合は、データを入れるだけでパラメータが簡単に求まるような数式はありません。そのため、まず初めにランダムなパラメータでモデルを作り、そのモデルによる予測値と実際のデータとの誤差を計算します。
そして、少しずつパラメータを変化させ、誤差が最も小さくなるようなパラメータを探索します。パラメータの探索は、誤差が小さくなるように探索する方法のほか、実際のデータが得られる確率が最も大きくなるような方法もあります。
このパラメータ探索のことを“学習”と呼ぶことがあるため、パラメータ探索をしていない線形回帰モデルは機械学習には含まれないとする見方があります。
ロジスティック回帰とは
では、ロジスティック回帰モデルとはどのようなモデルで、どのようなパラメータを学習するのでしょうか。
まずモデルは、「2つに1つの状態を取るデータが、他の変数の一次結合によって表現される」というものです。線形回帰分析では数値データを分析しましたが、ロジスティック回帰分析では「買ったor買っていない」や「見た・見ていない」といった2つに1つの状態を取るデータを分析します。
その後の「他の変数の一次結合によって表現される」という部分は線形回帰分析と同じですね。つまり、求めるパラメータは他の変数に掛けられる係数ということになります。
前回アイスクリームの売上分析で使用したデータを再度使用します。ただし、今回は売上ではなく、ある特定の顧客がアイスクリームを買うかどうかと、それに最高気温がどのように関係しているかを分析したいと思います。
ロジスティック回帰実践
次のCSVファイルには、2014の日ごとの最高気温とその日ある顧客がアイスクリームを買ったかどうかが記録されています。
こちらからダウンロードしてください。右クリックからデスクトップに保存できます。
早速データを読み込みの中身を見てみましょう。まずは上記ファイルをダウンロードしデスクトップに移動してください。
次にRStudioを立ち上げ、スクリプト画面に図のようにコマンドを打ち込みます。このとき、setwd()関数の中に使用PCのデスクトップを示すパスを記入してください。実行は、コマンドが記入された行を選択し「Ctrl+Enter」です。実行結果は下のコンソール画面に表示されます。
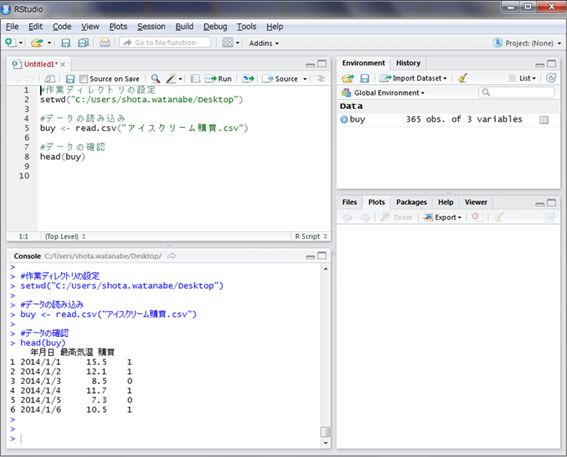
head()関数で6日分のデータを表示していますが、実際には日付、最高気温、購買が365日分入力されています。購買の列には、購入した場合は1、購入しなかった場合には0が記載されています。
まずは最高気温と購買の有無の関係をグラフで可視化してみましょう。
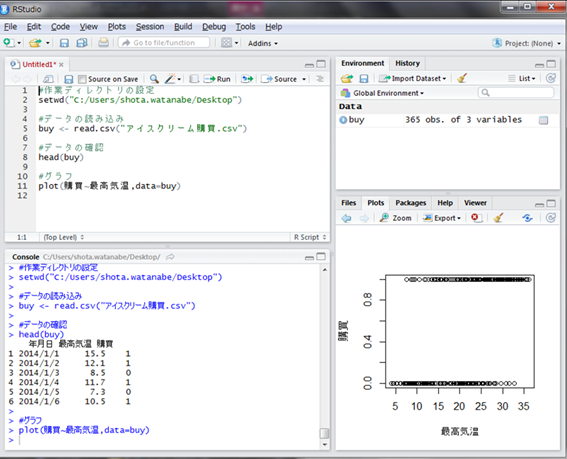
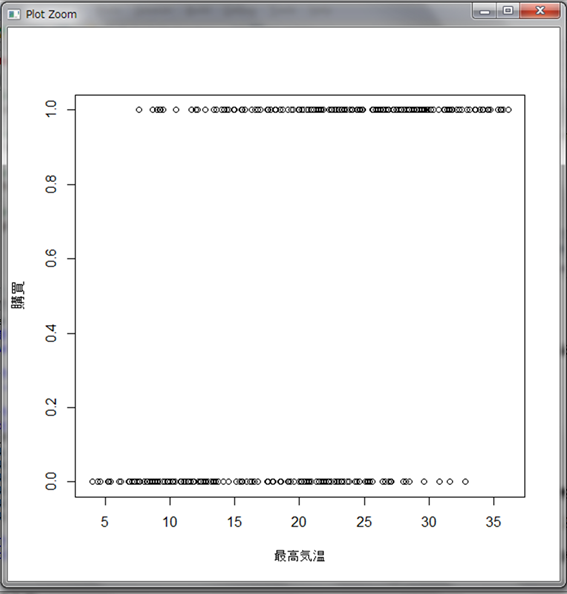
最高気温が低いと0が多く、高いと1が多いことが分かります。しかし、直線関係はないため線形回帰分析を行なうことはできません。
さて、線形回帰を行なうRの関数は次の関数でした。
- lm(目的変数の列名~説明変数の列名,data=データの変数名)
ロジスティック回帰を行なう場合は、glm()関数というものを使います。使い方は次の通りです。
- glm(目的変数の列名~説明変数の列名, data=データの変数名, family = binomial)
前半部分は線形回帰と全く一緒です。また、family = binomialという引数が追加されています。これでロジスティック回帰が実行できます。
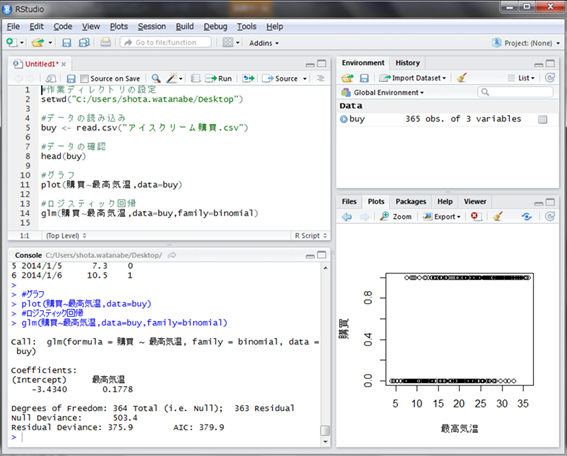
この結果の解釈は次のように考えます。
- (購買の確率)=1/(1+eー{(最高気温)×0.1778 - 3.4340})
なんとも不思議な式が出てきました。
まず左辺の(購買の確率)ですが、実はロジスティック回帰は購買が1になる確率を定式化するモデルだったのです。
線形回帰分析のときには数値データそのものを計算する式になりましたが、ロジスティック回帰では0か1かの値を計算するのではなく0と1の間の値を確率として計算します。
そして右辺の式ですが、これは変数の一次結合を0から1の間の数値に変換する役割を果たします。「(最高気温)×0.1778 - 3.4340」の部分は、最高気温の値によってどのような値もとりうることができます。
しかしそのままでは0と1を取る値に対してどのように解釈してよいか分かりません。そのため、この値をマイナス1倍し、eの肩に乗せ、1を足し、逆数を取ります。eはネイピア数と呼ばれる定数です。肩に乗せる操作は累乗を表します。
たとえば最高気温が高いとき、肩に乗せる値はマイナス1倍されるので小さい値になります。eの肩に乗せて1を足しても小さい値のままですが、逆数を取ることで大きな値になります。
仮に最高気温がマイナス無限大としましょう。すると、アイスクリームの購買確率は限りなく0に近づくと予想されます。実際、肩に乗る値はマイナス1倍され無限大となり、eの無限大乗に1を足しても無限大です。無限大の逆数は0となります。
一方最高気温が無限大になった場合、購買確率は限りなく1に近づくと予想されます。このとき肩に乗る値はマイナス無限大となります。eのマイナス無限大乗は0になります。結果、1/(1+0) = 1となり予想は当たりました。
次に、計算されたパラメータがどういう意味を持つのか考えてみます。最高気温に掛けられている0.1778というパラメータは、プラスならば変数の値が高いほど1になる確率が高く、マイナスならば1になる確率が低くなります。これは線形回帰分析と同じです。
ただし、最高気温が1度上がったからといって確率が0.1778大きくなるわけではありません。実は0.1778という数値だけではあまり意味がなく、この数値をeの肩に乗せた値、つまりe0.1778が重要です。
この値をRで計算してみましょう。exp()関数の引数に肩に乗せる数値を与えるだけです。
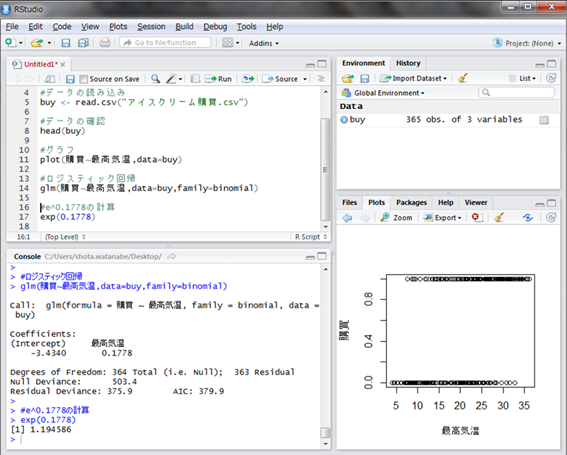
e0.1778は1.194586(約1.2)と計算されました。そしてこの数値の持つ意味は、「変数が1単位増えたときに、目的の変数が1である確率が増える割合」を表します。
つまり、最高気温が1度上昇すると購入確率が約1.2倍になるという意味です。eの肩に乗る値がマイナスのときは1より小さい値になるので、変数が1単位増えるごとに確率が減っていきます。
さて、前回lm()関数の結果の詳細を表示するsummary()を使用しましたが、glm()関数でもsummary()関数は使えます。実際に見てみましょう。
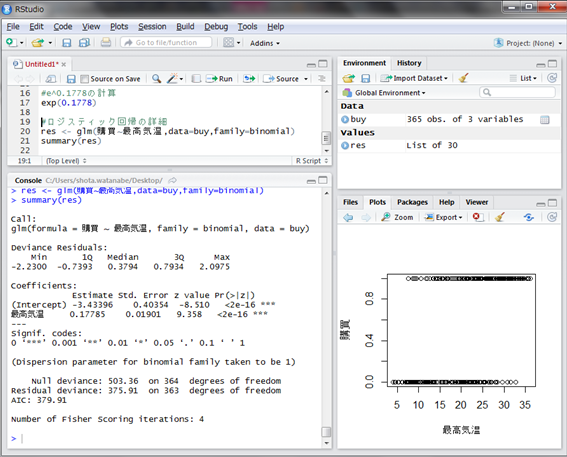
最高気温の行のPr(>|z|)という部分が<2e-16 ***となっていますが、これは係数が0である確率が非常に0に近く有意に差がある、という意味です。
統計的に見て、最高気温の係数0.1778は偶然0より大きいのではなく、有意に差があるということです。もし係数が偶然0より大きかっただけで、0の場合も十分ありえる場合、Pr(>|z|)の値が1に近い値になります。
係数が0ということは、その説明変数には説明力がなく、どんな値を取っても50%の確率で目的変数は0または1になるということになります。
さて、線形回帰分析の時には、データへの当てはまりの良さを表す決定係数(R2)という指標があったのですが、ロジスティック回帰のようなパラメータを探索する方法では決定係数を計算することができません。
では、どのようにモデルがデータに当てはまっているかを判断するのでしょうか。ロジスティック回帰は確率を定式化するモデルでした。つまり、説明変数から目的変数が1になる確率を計算することができます。
そこで、先ほど作成したモデルに対し最高気温から確率を計算してみましょう。それはpredict()関数で簡単に計算できます。引数に先ほどのモデルを与え、type=”response”と指定します。
※この指定がないと、eの肩に乗る値が計算されます。
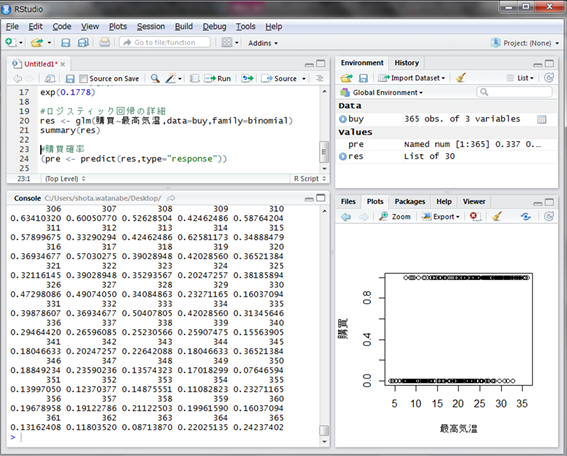
365個の購買確率が計算されました。縦軸を最高気温にしてグラフ化してみましょう。
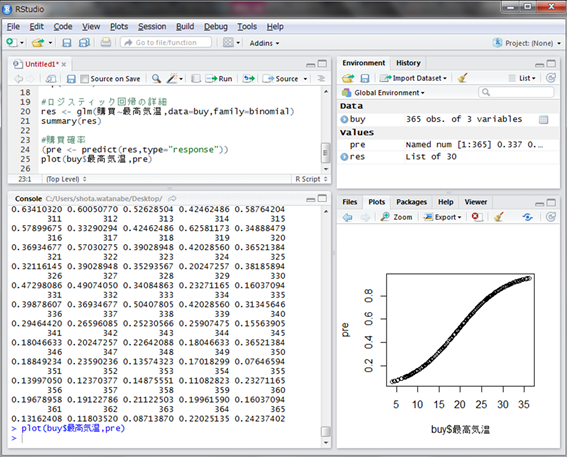
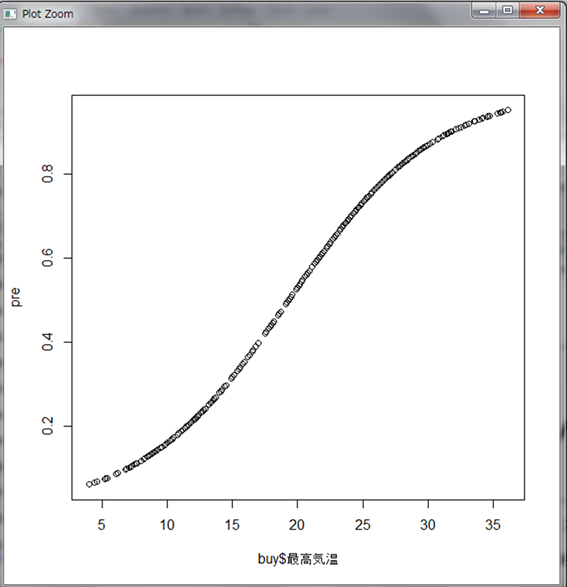
最高気温が低いと0に近く、最高気温が上がるにつれ1に近づいている様子が伺えます。
それでは、仮にこの確率が0.5未満なら0、0.5以上なら1というように判断してみましょう。その判断と実際の購買との正否から、正解率を出してみます。
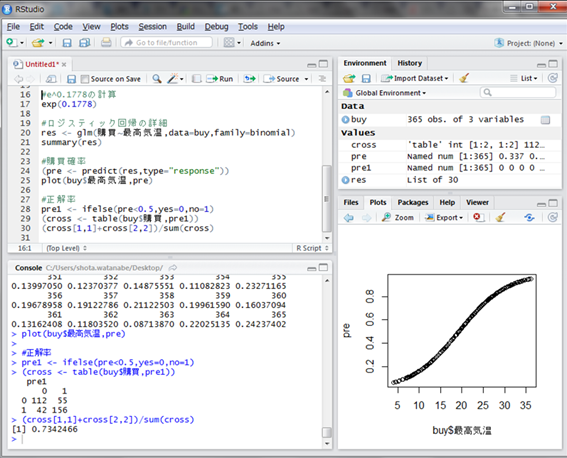
ifelse()関数はエクセルのIF関数のように使える便利な関数で、変数の各要素が条件に当てはまるときはyesの値を、そうでないときはnoの値を返す関数です。
次に、table()関数で購買と予測の集計表を作っています。最後に、購買結果と予測が合っている割合を計算しました。すなわち約73.4%の正解率ということになります。ランダムに予測した場合は50%の正解率になると考えられるので、まずまず結果ではないでしょうか。
以上がロジスティック回帰モデルの一通りの実践でした。なお、説明変数が2つ以上ある場合も全く同じようにロジスティック回帰モデルを作ることができます。
前回の重回帰分析のときに使用したstep()関数で変数の最適化もできます。前回のコラムを参考にしながら、ぜひ実際のデータを分析してみてください!
今回はここまで。次回はクラスター分析のお話をしたいと思います。
アサインナビでは、データサイエンスに関するセミナーを随時開催しております。
過去には、データサイエンティストの知識を習得するための実践塾や、特別講師を招いてのセミナーなどを開催しております。
過去の様子はこちらからご確認いただけます。
▼データサイエンティスト実践塾▼
第1回データサイエンティスト実践塾を修了しました!
▼データサイエンスの現状と未来▼
シリコンバレーに学ぶ、日本のデータサイエンスの現状と未来 ~これからのデータドリブンな時代に本当に必要なこと~を開催しました







